Question

A particle of mass m moves in the $XY$ plane with a velocity $v$ along the straight line $AB$ . If the angular momentum of the particle with respect to origin $O$ is ${L_A}$ and ${L_B}$ when it is at $A$ and ${L_B}$ when it is at $B$ , then:

A. ${L_A} < L$
B. ${L_A} > {L_B}$
C. ${L_A} = {L_B}$
D. The relationship between ${L_A}$ and ${L_B}$ depends upon the slope of the slope of the line $AB$.

Answer 1

In this question we will use the concept of momentum and we will take that in vector form to solve this problem whereas, In physics, angular momentum is a property that describes the rotatory inertia of an object moving around an axis that may or may not pass through it.

Formula used:
$L = mvr\sin \theta$
Where, $L$ is the angular momentum, $m$ is the mass of an object, $v$ is the linear velocity and $r$ is the radius.

Complete step by step answer:
Let us redraw the figure ,draw a perpendicular OP to the line and let d be the distance and join the line OA and proceed.From the definition of angular momentum, we know that, (considering in vector format)
$\vec L = \vec r \times \vec P = rmv\sin \phi ( - \vec k)$

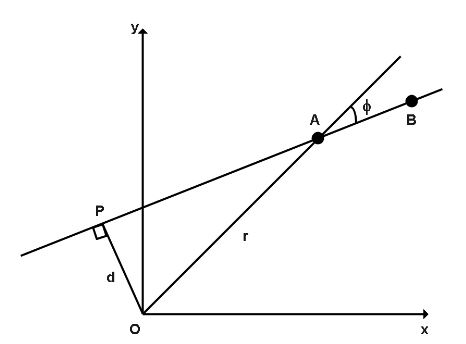
Therefore, the magnitude of $L$ is $L = mvr\sin \phi = mvd$ .
Whereas, $d = r\sin \phi$ which is the distance of the closest approach of the particle to the origin. As $d$ is the same for both.Hence,
${L_A} = {L_B}$
Or we can say that,
$\vec L = \vec r \times \vec P$ or $\vec L = \vec r \times m\vec V$
And according to the diagram,
$\vec L = \vec d \times m\vec V$
Whereas $\vec V$ is the velocity vector and we know that it is the same at both the given points $A$ and $B$. And $\vec d$ is a perpendicular vector on the velocity vector from the origin that is perpendicular on line $AB$ so, we can say that $\vec d$ is also the same in both cases.Hence, ${L_A} = {L_B}$

So, the correct option is C.

Note: Remember that angular momentum can also be formulated as the product of the moment of inertia (I) and the angular velocity (ω) of a rotating body. Here we can derive the equation.
$\vec L = I\vec \omega$
Where, $L$ is the angular momentum, $I$ is the rotational inertia and $\omega$ is the angular velocity.
The right-hand thumb rule designates the direction of the angular momentum vector in this situation, which is the same as the axis of rotation of the provided item.