Question

A particle of mass m just completes the vertical circular motion. Derive the expression for the difference in tension at the highest and the lowest points.

Answer 1

In vertical circular motion of a particle, we assume that for just completing the circle, the tension at the highest point is just zero, such that the centrifugal force due to circular motion just balances the weight of the particle at the highest point. After this, tension will be the function of the component of weight, in the direction of string and the centrifugal force on the particle.

Formula used:
$F_{centrifugal}= \dfrac{mv^2} {R}$, $K.E. = \dfrac12 mv^2$,$P.E. = mgh$

Complete step-by-step answer:
For completing the circle, the string must always be taut, otherwise after a certain point (when string becomes loose), the particle will perform a parabolic path. After giving ‘u’ velocity to a particle at rest, tied with the string, the minimum kinetic energy will be at the highest point, since at that point, most of the kinetic energy will get turned into potential energy. So, we shall start with the highest point.
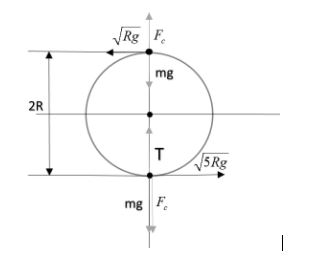
At the highest point, weight will act downward and centrifugal force upward and there will be no tension (as stated).
Hence at that point, $\dfrac{mv^2}R=mg$
Or $v= \sqrt{Rg}$

After this, lets apply energy conservation method to find the velocity at the bottom most point, which follows;
$K.E._{initial} + P.E._{initial}= K.E._{final}+P.E._{final}$
Taking bottom most point as reference , P.E. = 0
Hence, $\dfrac12 m{(\sqrt{Rg}})^2 + mg(2R) = \dfrac12mv^2$+ 0
$\Rightarrow \dfrac12 mgR+2mgR=\dfrac12 mv^2$
$\Rightarrow \dfrac52 mgR = \dfrac12 mv^2$
$\Rightarrow v= \sqrt{5gR}$
Now, writing force equation at the bottom most point;
$T= F_{c} + mg$
$T= \dfrac{mv^2} R + mg$
$T= \dfrac{m{(\sqrt{5gR})}^2} R + mg$= $5mg + mg = 6mg$
Hence, tension at lower point is $\ 6mg$ and as discussed at uppermost point is zero.
Hence the difference in tensions between uppermost and bottom point is 0 -$\ 6mg$= -$\ 6mg$

Note: The chance of mistake here is that the student assumes velocity at the uppermost point to be zero as to just complete the circle. But doing that will cause the motion of the particle as parabolic from that point, i.e. half circle and half parabolic. If preceded that way, the result will come out to be wrong. Hence one should visualize the question properly and then proceed by drawing a diagram.