Question

A particle of mass M is situated at the center of a spherical shell of mass and radius a. The magnitude of gravitational potential at a point situated at a/2 distance from the center will be:
(A) $\dfrac{2GM}{a}$
(B) $\dfrac{3GM}{a}$
(C) $\dfrac{4GM}{a}$
(D) $\dfrac{GM}{a}$

Answer 1

As we know that the potential in the interior of the spherical shell does not change so adding the potential of the spherical shell to the potential generated by the mass at the center gives the potential at the required point.

Formula used: $V=\dfrac{GM}{r}$
Here, V is the gravitational potential of the spherical shell of mass M and radius r, G is the gravitational constant.

Complete step by step answer:
Let P be the point at a distance a/2 from the center of the spherical shell where gravitational potential is needed to be found.

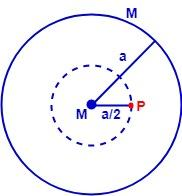
Potential at point P due to spherical shell is given by:
$\Rightarrow V_sphere=\dfrac{GM}{a}$ (Potential is same at every point inside the shell)
Potential at point P due to the particle of mass M at the center is given by:
$\Rightarrow V_particle=GM$ (Here, a/2 is the distance of point P from the mass M)
Total gravitational potential at point P = Sum of all potentials
i.e.
$\Rightarrow V_P=V_sphere+V_particle$
$\begin{aligned} &\Rightarrow\dfrac{GM}{a}+\dfrac{GM}{{}^{a}/{}_{2}} \\\ &\Rightarrow\dfrac{GM}{a}+\dfrac{2GM}{a} \\\ &\Rightarrow\dfrac{3GM}{a} \\\ \end{aligned}$.

Note:
Do not confuse the electric field of the spherical shell with the potential inside it. As the electric field inside is zero so using the relation $E=-\dfrac{dV}{dx}$ we find that the potential at the surface and inside the shell is same and constant.