Question

A particle of mass m is projected with a velocity $v$ making an angle of 45° with the horizontal. The magnitude of the angular momentum of the projectile about the point of projection when the particle is at maximum height h is:
A. Zero
B. $\dfrac{m{{v}^{3}}}{4\sqrt{2}g}$
C. $\dfrac{m{{v}^{3}}}{\sqrt{2}g}$
D. $m\sqrt{3g{{h}^{3}}}$

Answer 1

Hint: When you throw at a particle in a projectile, the horizontal velocity remains constant throughout the time of flight. The vertical velocity is first decelerated and then accelerated due to the gravitational acceleration. Find the height of the maximum point and the linear momentum at that point. Angular momentum will be the multiplication of these two quantities.

Formula Used:

The relation between travelled distance, final velocity, and initial velocity is given by,
${{v}^{2}}={{u}^{2}}+2as$

Where,
$s$ is the distance travelled by the particle,
$u$ is the initial velocity
$v$ is the final velocity
$a$ is the acceleration

Linear momentum is given by,
$p=mv$

Where,
$m$ is the mass of the particle
$v$ is the linear velocity

Angular momentum is given by,
L = angular momentum = Momentum ✕ Perpendicular Distance

Complete step by step answer:
Let’s look at the diagram to understand the motion of the particle,

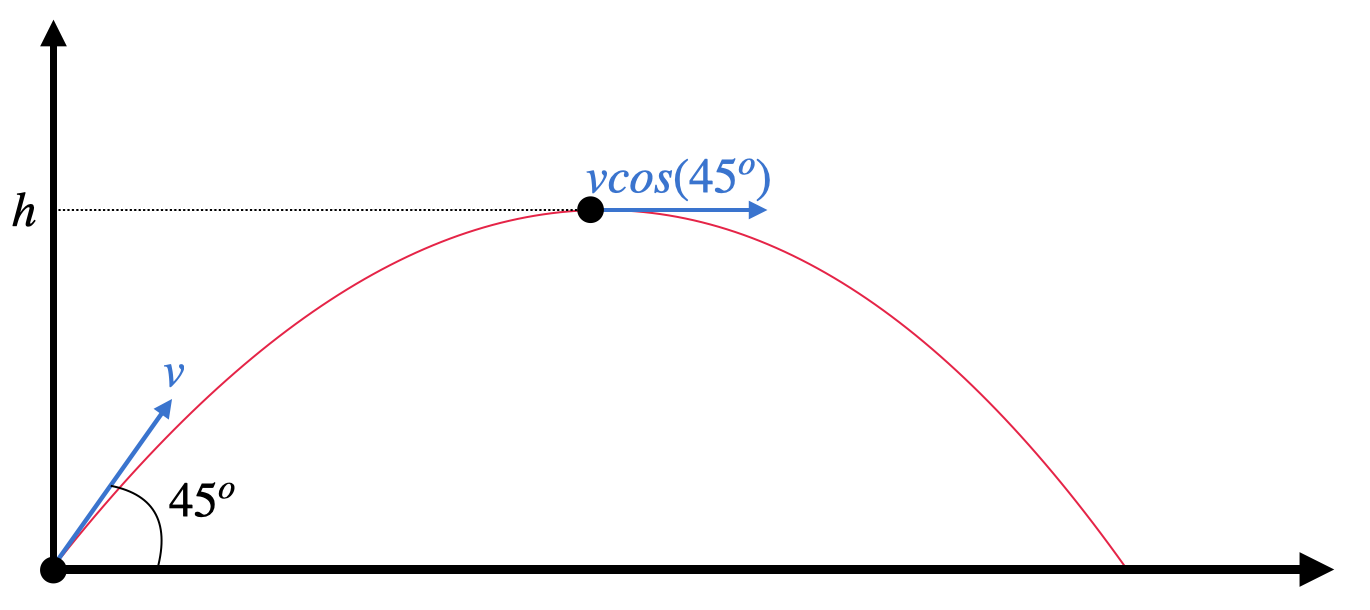
We can divide the velocity of the particle into two components -
$v\cos (45)$ in the horizontal direction
And
$v\sin (45)$ in the vertical direction

There is no force in the horizontal direction. So, there won’t be any change in the horizontal component of the velocity.
However, the vertical component of the velocity will undergo retardation till it reaches the highest point.

Let’s assume that the highest point is at a height of h.

Hence, we can write that,
${{v}^{2}}={{u}^{2}}+2as$
$\Rightarrow 0={{(v\sin 45)}^{2}}-2gh$
$\Rightarrow h=\dfrac{{{(v\sin (45))}^{2}}}{2g}$
$\Rightarrow h=\dfrac{{{v}^{2}}}{4g}$

So, the highest height is,
$\dfrac{{{v}^{2}}}{4g}$

Now, the momentum at the highest point will only be the momentum due to the horizontal component as the vertical component is zero.

Hence, linear momentum at height h is,
$p=mv\cos 45$

From the definition of angular momentum, we can write,

Angular Momentum = Linear Momentum $\times$ the perpendicular distance of linear momentum vector from the axis.

Hence, we can write,
$L=ph$
$\Rightarrow L=(\dfrac{mv}{\sqrt{2}})(\dfrac{{{v}^{2}}}{4g})$
$\Rightarrow L=(\dfrac{m{{v}^{3}}}{4\sqrt{2}g})$
So, the required angular momentum of the particle is given by,
$L=(\dfrac{m{{v}^{3}}}{4\sqrt{2}g})$

Hence, the answer is (B).

Note: The angular momentum is a vector quantity. It is given by,
$\overrightarrow{L}=\overrightarrow{r}\times \overrightarrow{p}$
However, in this problem, we did not have to use vector multiplication as the velocity vector was only in the horizontal direction. Otherwise, we had to use the vertical component as well.