Question

A particle of mass m is moving in x-direction with speed 2v hit by another particle of mass 2m moving in the y-direction with speed v. If the collision is perfectly inelastic, the percentage of the energy retained by the colliding particles after the collision is close to
(a){\text{ 56% }} \\\ (b){\text{ 80% }} \\\ (c){\text{ 35% }} \\\ (d){\text{ 44% }} \\\

Answer 1

Hint – In this question write the kinetic energy of a particle moving in the x-direction and then the kinetic energy of the second particle moving along y-direction. Using this, find the total kinetic energy before the collision, then after the collision, find the combined velocity of the particles, this will help getting the final kinetic energy. The percentage energy retained will simply be Energy retained =$\dfrac{{{{\left( {K.E} \right)}_{initial}} - {{\left( {K.E} \right)}_{final}}}}{{{{\left( {K.E} \right)}_{initial}}}} \times 100$. This will help getting the answer.

Complete step-by-step solution -
__

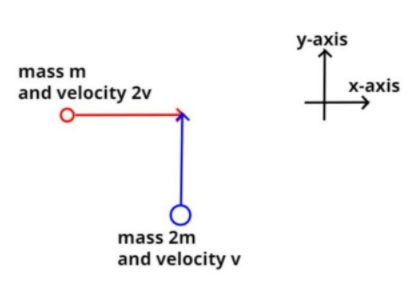
Elastic collision – An elastic collision is the collision of two or more particles such that after collision the total kinetic energy of the particles remains the same. For elastic collision the coefficient of restitution (e) is 1.
Inelastic collision – An inelastic collision is the collision of two or more particles such that after collision the total kinetic energy of the particles does not remains same i.e. the kinetic energy of the particles are lost, in this case the coefficient of restitution (e) is less than 1 and greater than zero.
In a perfectly inelastic collision the maximum amount of kinetic energy is lost and in this case the coefficient of restitution is zero (0), so the final kinetic energy is given as,
${\left( {K.E} \right)_{final}} = \dfrac{1}{2}\left( {{m_1} + {m_2}} \right){\left( {{V_f}} \right)^2}\left( {1 - {e^2}} \right)$, where ${V_f}$ is final velocity after collision, e = coefficient of restitution which is zero for perfectly inelastic collision, and $\left( {{m_1} + {m_2}} \right)$ is the combined mass of the particles after collision.

Given data:
Mass of first particle ${m_1}$ = m, mass of second particle ${m_2}$ = 2m.
Velocity of first particle = 2v, velocity of second particle = v.
Now it is given that the first particle is moving in x-direction and the second particle is moving in y-direction.
Now as we know that kinetic energy (K.E) of particle is
$\Rightarrow K.E = \dfrac{1}{2}M{V^2}$, where M = mass, V = velocity
So initial K.E of first particle is
$\Rightarrow {\left( {K.E} \right)_1} = \dfrac{1}{2}\left( m \right){\left( {2v} \right)^2} = 2m{v^2}$
And initial K.E of second article is
$\Rightarrow {\left( {K.E} \right)_2} = \dfrac{1}{2}\left( {2m} \right){\left( v \right)^2} = m{v^2}$
So total initial K.E is
$\Rightarrow {\left( {K.E} \right)_{initial}} = {\left( {K.E} \right)_1} + {\left( {K.E} \right)_2}$
$\Rightarrow {\left( {K.E} \right)_{initial}} = 2m{v^2} + m{v^2} = 3m{v^2}$
Now it is given that the first particle is hit by a second particle and the collision is perfectly inelastic.
So the combined velocity is
$\Rightarrow V = \dfrac{{{m_1}{v_1}\hat i + {m_2}{v_2}\hat j}}{{{m_1} + {m_2}}}$ (where, $\hat i{\text{ and }}\hat j$are the direction of x and y respectively)
Now substitute the values in above equation we have,
$\Rightarrow V = \dfrac{{2mv\hat i + m\left( {2v} \right)\hat j}}{{2m + m}} = \dfrac{{2v}}{3}\left( {\hat i + \hat j} \right)$
Now take the modulus of this we have,
$\Rightarrow \left| V \right| = \dfrac{{2v}}{3}\left| {\left( {\hat i + \hat j} \right)} \right| = \dfrac{{2v}}{3}\sqrt {{1^2} + {1^2}} = \dfrac{{2\sqrt 2 v}}{3}$
So the final velocity of the combined particle is
$\Rightarrow {V_f} = \dfrac{{2\sqrt 2 v}}{3}$
So the final K.E of the combined particle is
$\Rightarrow {\left( {K.E} \right)_{final}} = \dfrac{1}{2}\left( {{m_1} + {m_2}} \right){\left( {{V_f}} \right)^2}\left( {1 - {e^2}} \right)$, where (e) is coefficient of elasticity or coefficient of restitution, whose value is, e = 0 for perfectly inelastic and e = 1 for perfectly elastic).
So substitute the values we have,
$\Rightarrow {\left( {K.E} \right)_{final}} = \dfrac{1}{2}\left( {2m + m} \right){\left( {\dfrac{{2\sqrt {2v} }}{3}} \right)^2}\left( {1 - 0} \right) = \dfrac{4}{3}m{v^2}$
Now the energy retained by the colliding particles is the ratio of difference of initial and final K.E to initial K.E multiplied by 100.
Energy retained = $\dfrac{{{{\left( {K.E} \right)}_{initial}} - {{\left( {K.E} \right)}_{final}}}}{{{{\left( {K.E} \right)}_{initial}}}} \times 100$
Now substitute the values we have,
Therefore, energy retained = $\dfrac{{3m{v^2} - \dfrac{4}{3}m{v^2}}}{{3m{v^2}}} \times 100 = \dfrac{5}{9} \times 100 = 55.55 \simeq 56$ %.
So this is the required answer.

Note – The trick point in this question is about the concept of perfectly inelastic collision, in such a type of collision the maximum amount of kinetic energy of a system is lost. We have taken into consideration the combined velocities of the particles after the collision as in this type of collision the particles stick together and the coefficient of restitution is simply zero in this case.