Question

A particle of mass m is moving in the potential
$V(x) = \begin{cases} V_0 + \frac{1}{2} m \omega_{0P}^2 x^2 & \quad \text{if } x > 0 \\\\\infty & \quad \text{if } x \leq 0 \end{cases}$
Figures P, Q, R, and S show different combinations of the values of $\omega_0$ and $V_0$.

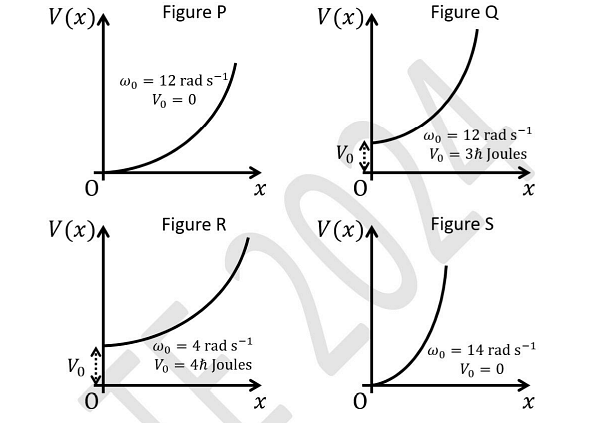
Let $E^{(P)}_j$, $E^{(Q)}_j$, $E^{(R)}_j$, and $E^{(S)}_j$ with $j = 0, 1, 2, \ldots$, be the eigen-energies of the j-th level for the potentials shown in Figures P, Q, R, and S, respectively. Which of the following statements is/are true?

• A. $E^{(P)}_0 = E^{(Q)}_0$
• B. $E^{(Q)}_0 = E^{(S)}_0$
• C. $E^{(P)}_0 = E^{(R)}_0$
• D. $E^{(R)}_0 \neq E^{(Q)}_0$

Answer 1

Answer: (B), (C), (D)

$E^{(Q)}_0 = E^{(S)}_0$

Answer 2

The correct Answers are (B):$E^{(Q)}_0 = E^{(S)}_0$,(C):$E^{(P)}_0 = E^{(R)}_0$,(D):$E^{(R)}_0 \neq E^{(Q)}_0$