Question
Question: A particle of mass \(m\) is moving in a plane along a circular path of radius \(r\). its angular mom...
A particle of mass m is moving in a plane along a circular path of radius r. its angular momentum along the axis of rotation is L. the centripetal force acting on the particle is:
A. mrL2
B. rL2m
C. mr3L2
D. mr2L2
Solution
The concept to be used here is of angular momentum and its formula and how it can be changed to represent the centripetal force which is acting on the particle.
Shuffle the terms in the formula of angular momentum and bring it in the form of any one term present in the formula of centripetal force.
Then substitute the whole value of the term in the formula of centripetal force and solving it will give the required answer.
Complete step by step answer:
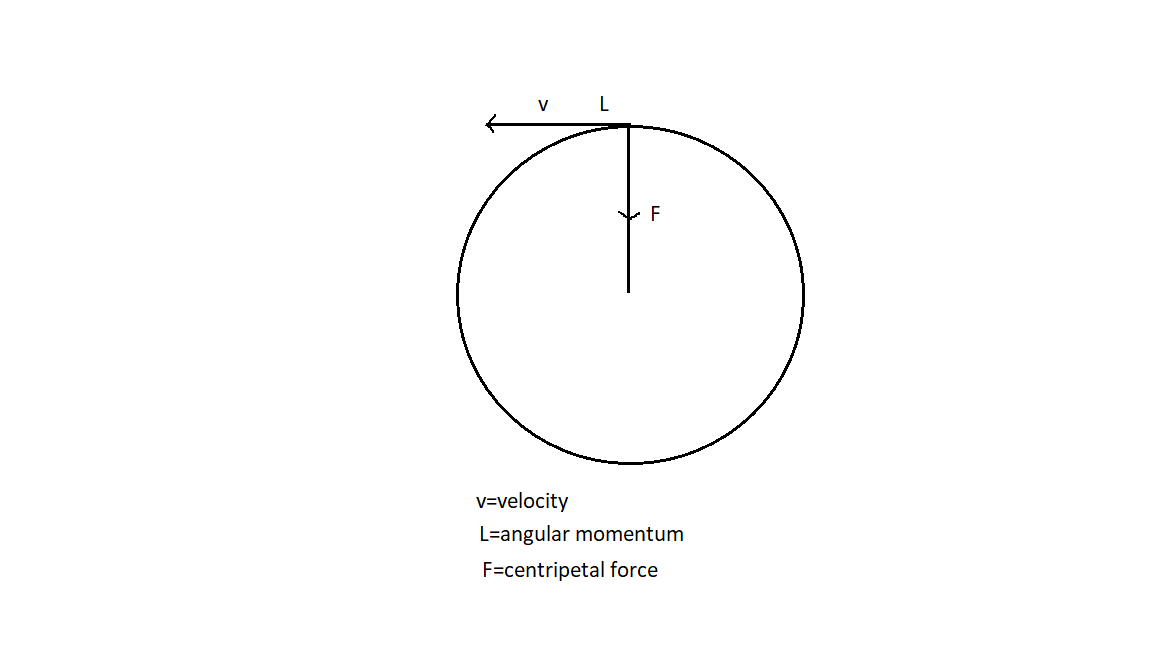
We can see in the figure that the body is moving in a circular path with velocity perpendicular to the centripetal force. Also, it has angular momentum L which can be found using its formula as velocity is perpendicular to position vector which is radius from the rotating axis so momentum vector is perpendicular to radius vector so
L=rpsinθ where r→is position vector and p→ is linear momentum
andθ is the angle between both which in our case is 900.
So L=m×v×r......(1)
And centripetal force
F=rmv2
Replacing value of v from (1)
v=mrL
Now putting this value in centripetal force equation to find its value in terms of angular momentum
F=rm(mrL)2=mr3L2......(2)
So, we can see that centripetal force is expressed in terms of angular momentum and the correct option is C.
Note:
Angular momentum can be expressed for both linear and rotational motion as well as for both combined too. L=I×w where I is moment of inertia and w is angular velocity of rotational motion.
Centripetal force is the force responsible for rotating a body in a circular motion.it arise due to other forces which act on the body in a circular path. Its direction is always towards the centre. It also gives rise to centripetal acceleration.
Centrifugal force is opposite in direction to centripetal force but equal in magnitude.it is a fictitious force.
