Question

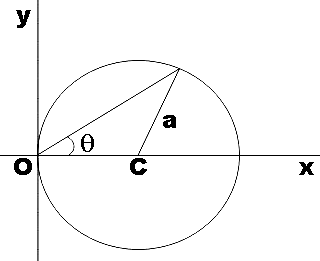
A particle of mass m is moving in a circular path of radius $a$ with a constant velocity v is shown in the figure. The center of circle is marked by ‘C’. The angular momentum from the origin O can be written as:

A.$mva\left( 1+\cos 2\theta \right)$
B.$mva\left( 1+\cos \theta \right)$
C.$mva\cos 2\theta$
D.$mva$

Answer 1

As a first step, we could recall the expression for angular momentum. Then, you could make necessary constructions in the given diagram and thus obtain the necessary components that are required to be substituted in that expression. Now, directly substitute and get the answer.

Formula used:
Angular momentum,
$L=mvr$

Complete Step by step solution:
In the question we are given a particle of mass m moving along a circular path with centre C that has radius $a$ with constant velocity v as shown in the figure. We are supposed to find the angular momentum of the particle about origin O.
Let us recall that the magnitude of angular momentum of any orbiting particle is equal to the product of its linear momentum $(mv)$ and the perpendicular distance r, that is,
$L=mvr$ ……………………………………… (1)
Now let us do necessary construction in the given figure.

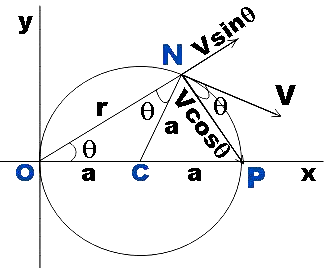
We have considered a point N at r distance from the origin and v is the tangential velocity at that point. We have also resolved this velocity into its components. Clearly, the cosine component of the velocity is responsible for the angular momentum about the origin.
Now consider$\Delta NOP$,
$\cos \theta =\dfrac{r}{2a}$
$\Rightarrow r=2a\cos \theta$ ……………………………………………. (2)
‘$v$’ which is the linear velocity causing the angular momentum will be,
$v=v\cos \theta$ …………………………………………….. (3)
Now we could directly substitute (2) and (3) in (1) to get,
$L=m\left( v\cos \theta \right)\left( 2a\cos \theta \right)$
$\Rightarrow L=mva\left( 2{{\cos }^{2}}\theta \right)$
But, $2{{\cos }^{2}}\theta =1+\cos 2\theta$
$\therefore L=mva\left( 1+\cos 2\theta \right)$
Therefore, we found that the angular momentum from the origin O can be written as,
$L=mva\left( 1+\cos 2\theta \right)$

Hence, option A is found to be the correct answer.

Note:
You may have noticed that we have not considered the sine component of velocity while solving. This is because, we are finding the angular momentum from the origin O and the sine component is not perpendicular to that point to be responsible for the angular momentum. Also, we have used basic geometry for identifying the angles.