Question

A particle of mass m is moving along the side of a square of side ‘a’, with a uniform speed v in the x-y plane as shown in the figure. Which of the following statements is false for the angular momentum $\vec{L}$ about the origin.

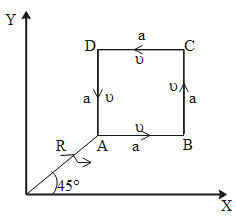
A. $L=-\dfrac{mv}{\sqrt{2}}R\hat{k}$ when the particle is moving from A to B
B. $L=mv\left[ \dfrac{R}{\sqrt{2}}-a \right]\hat{k}$ when the particle is moving from C to D
C. $L=mv\left[ \dfrac{R}{\sqrt{2}}+a \right]\hat{k}$ when the particle is moving from B to C
D. $L=\dfrac{mv}{\sqrt{2}}R\hat{k}$ when the particle is moving from D to A

Answer 1

The angular momentum of a particle is the cross product of the position vector and angular momentum. Cross product of two vectors produces a vector quantity which has a direction perpendicular to both the vector quantities. The position vector of the body is considered from the reference point (origin) to the point where the object is placed.

Complete answer:
It is mentioned in the question that an object is moving in a square orbit in the x-y plane. As the position of the object changes the position vector of the object also changes.
So for the given question, we can divide the whole path covered by the object into 4 sections.
The case I: (object moving from terminal A to B)
If we consider the object is at point somewhere in point A and B. and extend the direction the line AB to a point where it meets the y-axis,

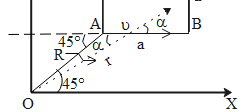
So, when the object is moving from point A to B the angular momentum of the body can be given as,
$\begin{aligned} & \vec{L}=\vec{r}\times \vec{P} \\\ & \Rightarrow \left| {\vec{L}} \right|=\left| r \right|\left| P \right|\sin \alpha \\\ & \Rightarrow \left| {\vec{L}} \right|=(r\sin \alpha )P \\\ \end{aligned}$
They represent the perpendicular distance between the origin of the XY axis and the extended path AB. This distance can also be represented as $\left( R\sin 45{}^\circ \right)$
$\begin{aligned} & r\sin \alpha =R\sin 45{}^\circ \\\ & \Rightarrow \vec{L}=P\left( R\sin 45{}^\circ \right) \\\ & \Rightarrow \vec{L}=\left( mv \right)\left( -\dfrac{R}{\sqrt{2}} \right) \\\ & \Rightarrow \vec{L}=-\dfrac{R}{\sqrt{2}}mv\quad .......\left( 1 \right) \\\ \end{aligned}$
Case II: (object moving from terminal C to D)
If we consider the object is moving from point C and D. and extend the direction of the line CD to a point where it meets the X-axis,

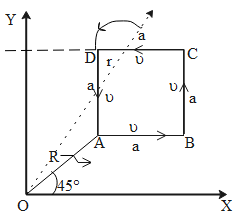
When we take the direction of the cross product of the position vector and the position vector the direction of the angular momentum would be towered by the positive z-axis.
$\vec{L}=+ve\quad .....\left( 2 \right)$
Case III: (object moving from terminal B to C)
If we consider the object is moving from point B to C. and extend the direction of the line BC to a point where it meets the Y-axis,

The angular momentum of the object can be given as,
$\left| {\vec{L}} \right|=\dfrac{R}{\sqrt{2}}mv$
The direction of the angular momentum will be towards the positive Z-axis
$\vec{L}=+ve\quad ....(3)$
Case IV: (object moving from terminal D to A)
If we consider the object is moving from point D to A. and extend the direction of the line BC to a point where it meets the Y-axis,

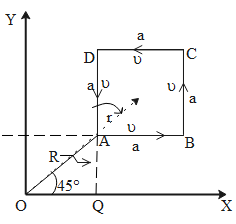
The direction of the angular momentum will be towards the positive –Z-axis or (-k). So, the angular momentum can be given as,
$L=-\dfrac{mv}{\sqrt{2}}R\hat{k}\quad ....\left( 4 \right)$

Thus, from the above discussion, it can be noted that the correct option which satisfies the question will be Option D.

Note:
The cross product is only possible between two vector quantities. Vector quantities have magnitude as well as a particular direction. The direction of the resultant vector in a cross product can also be found by the right-hand rule.