Question

A particle of mass m is kept on the top of a sphere of radius R. It is given a sharp impulse, which imparts it a horizontal speed v.(a)Find the normal force between the sphere and particle just after impulse. (b)what should be the minimum value of v for which the particle does not slip on the sphere? (c) Assuming the velocity v to be half the minimum calculated in part (b) find the angle made by the radius.

Answer 1

The particle experiences centrifugal force which is balanced by its weight mg. First, we find this balancing equation and then further proceed with the question where the relation between angle and the radius of the sphere is used to solve the question.
Formula used-
$N = mg - \dfrac{{m{v^2}}}{R}$
$\dfrac{{m{v^2}}}{R} = mg$
$\dfrac{{m{v^2}}}{R} = mg\cos \theta$

Complete step-by-step solution:
The sphere is a 3-D geometrical shape like a ball. It has a radius, area, and volume.

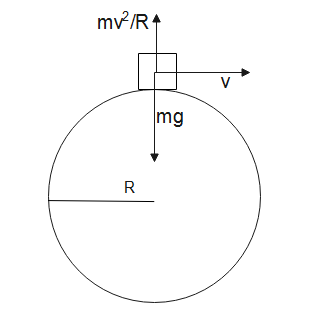
a). Let the radius be R, horizontal speed is v.
As we know that the normal force acting here is given by:
$N = mg - \dfrac{{m{v^2}}}{R}$
Therefore, here the normal force between the sphere and particle just after the impulse is given by N.
(b) We know when the particle is given maximum velocity, the centrifugal force balances the weight, and thereby, the particle does not slip on the sphere.
This is given by equation:
\eqalign{ & \dfrac{{m{v^2}}}{R} = mg \cr & \Rightarrow v = \sqrt {gR} \cr}
Therefore, here v is the minimum value of velocity for which the particle does not slip on the sphere.
(c) We can get the expression for the velocity the body is given:
\eqalign{ & {v_1} = \dfrac{{\sqrt {gR} }}{2} \cr & {v_1}^2 = \dfrac{{gR}}{4} \cr}
Now, in this case, when the particle loses contact with surface the velocity is given by:

\eqalign{ & \dfrac{{m{v^2}}}{R} = mg\cos \theta \cr & \Rightarrow v_2^2 = Rg\cos \theta .......(1) \cr & \dfrac{1}{2}mv_2^2 - \dfrac{1}{2}mv_1^2 = mgR(1 - \cos \theta ) \cr & \Rightarrow v_2^2 = v_1^2 + 2gR(1 - \cos \theta )...........(2) \cr & \cr}
From equation (1) and (2),
\eqalign{ & Rg\cos \theta = \dfrac{{Rg}}{4} + 2gR(1 - \cos \theta ) \cr & cos\theta = \left( {\dfrac{1}{4} + 2 - 2cos\theta } \right) \cr & \Rightarrow 3cos\theta = \left( {\dfrac{9}{4}} \right) \cr & \Rightarrow \theta = {\cos ^{ - 1}}\left( {\dfrac{3}{4}} \right) \cr & \cr}
Therefore, the angle made by the radius through the particle with the vertical when it leaves the sphere is given by the above result.
Additional information:
The radius is half of the diameter. The volume of the sphere is given by 4/3 times the pi constant times the cube of the radius. The entire sphere has a solid angle of 4 times the pi constant. The unit of solid angle is square radian (sr).
Further, we know that when we apply force F on any object, the object experiences other forces as well. These forces balance each other, as shown in the following figure:

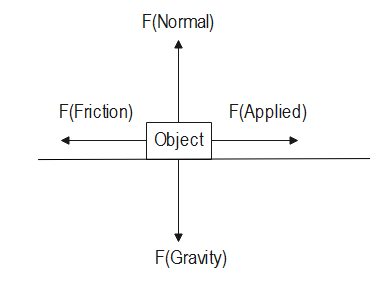
Here, if the velocity of the object is constant then the net force will be zero.

Note: The particle experiences a centrifugal force on it which is balanced by its weight; if this force is not balanced then the particle may fall from the surface of the sphere. Also, the initial velocity of a particle changes when the particle is given a sudden velocity.