Question
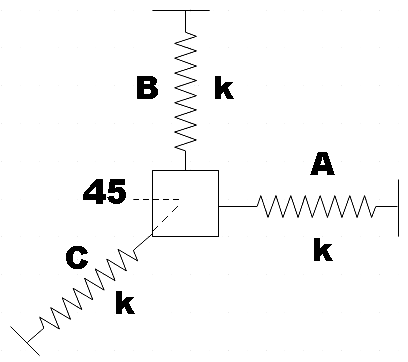
Question: A particle of mass m is attached with three springs A, B and C of equal force constants k as shown i...
A particle of mass m is attached with three springs A, B and C of equal force constants k as shown in the figure. The particle is pushed slightly against the spring C and released, the time period of oscillation will be:
A.2πkm
B.2π2km
C.2π3km
D.2π5km
Solution
Firstly, you could assign the restoring forces along each of the strings. Then, you could resolve these forces as per requirement and balance them. Thereby, you will be able to find the effective force constant of the system. You could substitute it in the expression for the time period of oscillation and thus get the answer.
Formula used:
Time period of oscillation,
T=2πkeffm
Complete answer:
In the question, we are given a particle of mass m that is attached to three springs A, B and C and all three springs have the same force constant k. So, this particle is being pushed against C and then released. We are asked to find the time period of oscillation for the system.
In order to answer the given question, firstly, we have to find the net force acting on the system.
Let x be the distance at which the particle pushed against C and the resultant elongation (y) will be the same for all three strings. We could depict the situation in the following diagram,
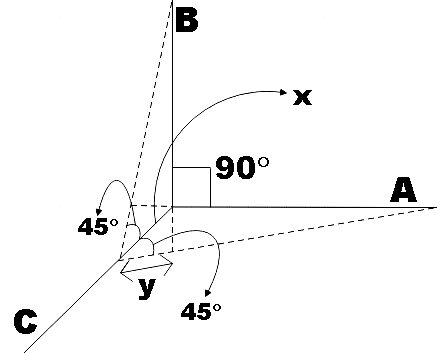
Now we have restoring forces in each string directed opposite to the elongation. And the restoring forces in strings A and B can be resolved into their horizontal and vertical components. Both their sine components get cancelled as they are directed opposite to each other.
From the figure, we see that,
y=xcos45∘ …………………………………… (1)
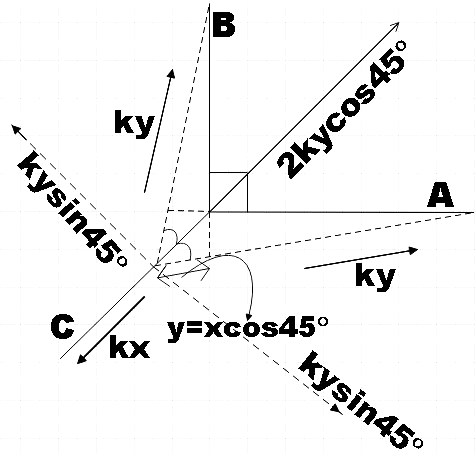
So the net force on the particle now will be,
Fnet=FC−2kycos45∘
⇒Fnet=−kx−2kycos45∘=−(kx+2kycos45∘)
Substituting (1), we get,
Fnet=−(kx+2kxcos45∘.cos45∘)
⇒Fnet=−kx(1+(2)×(21)2)
∴Fnet=−2kx
But we know that,
Fnet=−Keffx
Comparing the two equations, we get the effective spring constant as,
Keff=2k …………………………………. (2)
Now, we could recall the expression for the time period of oscillation which is given by,
T=2πkeffm
Substituting (2) we get,
T=2π2km
Therefore, we found the time period of oscillation of the system after the particle being pushed against string C as,
T=2π2km
Hence, option B is found to be the right answer.
Note:
According to Hooke’s law, the restoring force is proportional to the displacement of the string, that is,
F∝x
So,
F=−kx
Where, k is the force constant and the negative sign indicates that the force is directed in the direction opposite to the elongation caused. Knowledge of this law is the basic requirement for solving these kinds of problems.
