Question
Question: . A particle of mass m is attached to the ceiling of a cabin with an inextensible light string of le...
. A particle of mass m is attached to the ceiling of a cabin with an inextensible light string of length l The cabin is moving upward with an acceleration a. The particle is taken to a position such that string makes an angle θ with vertical. When the string becomes vertical, find the tension in the string.
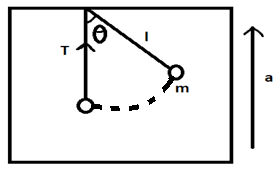
Solution
To calculate the tension, we can consider the frame of the cabin where both acceleration of object and acceleration due to gravity will have the same direction. We can use the law of conservation of energy to get the relationship between various quantities. Then using the fact that the net force acting on the new position will provide the centripetal force, we can find the value of T.
Formulas to be used:
Work=FDcosθ
Potential energy = mgeffh
Kinetic energy = 21mv2
Centripetal force = rmv2 (here r = l)
Complete step by step answer:
For calculating the tension, we need to move into the frame of the cabin, where along with gravitational force, acceleration will also act downward as a pseudo force which acts on all the bodies.
The effective acceleration due to gravity can be given as:
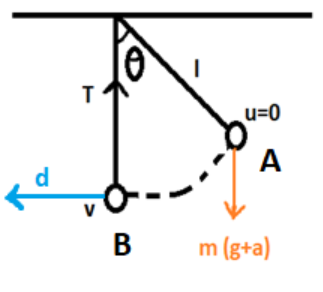
geff=(g+a) ______ (1) [ as both are in same downward direction]Work done by the force of tension in changing the position from A to B:
At A the initial velocity (u) is zero (because it is at rest in the beginning) at B, the final velocity becomes v.
The direction of tension is upwards while that of displacement (d) is towards left of B and the angle between them is 90°
Work = Force (F). Displacement (D)
Or
Work=FDcosθ
Work = 0 (∵θ=90o⟹cos90o=0)
Thus work done by tension is zero.
Now, according to law of conservation of energy, one form of energy gets converted to another so:
Decrease in potential energy = Increase in kinetic energy ________ (2)
Potential energy = mgeffh
Kinetic energy = 21mv2
Substituting in (2):
mgeffh=21mv2 ⟹v2=2geffh ⟹v=2geffh
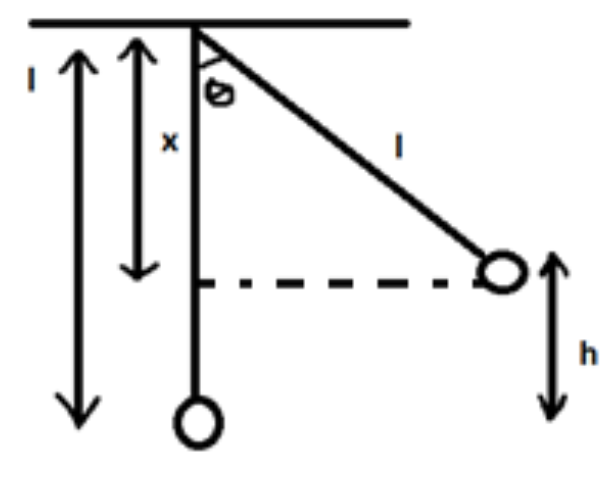
Calculating the value of h by recreating diagram specifically to find the height:
length h = length l – length x ____ (a)
Calculating cosθ in the formed triangle:
cosθ=HB here,
Base (B) = x Hypotenuse (H) = l
Substituting:
cosθ=lx x=lcosθ
Substituting in (a) to calculate h:
h=l−x ⟹h=l−lcosθ ⟹h=l(1−cosθ)
And value of geff from (1) is:
geff=(g+a)
Now substituting both the values in that of v, we get:
v=2geffh ⟹v=2(g+a)l(1−cosθ)
As mgeff is acting downward on A, it will act in the same way at B. Tension and this force are opposite in directions. This net provides the centripetal force, so:
T−mgeff=lmv2 [since centripetal force is lmv2]
Calculating the value of T by substituting all the known values:
T=mgeff+lmv2 ⟹T=m(g+a)+lm[2(g+a)l(1−cosθ)] ⟹T=m(g+a)+2m(g+a)(1−cosθ) ⟹T=m(g+a)[1+2(1−cosθ)] ∴T=m(g+a)[3−2cosθ]
Hence,when the string becomes vertical the tension in the string is m(g+a)[3−2cosθ].
Note:
When the two forces acting on the same point are opposite in directions, the net force will be the difference between them whereas when they are same in direction, the net force will be their sum.
For an angle, the perpendicular is the edge opposite to it and hypotenuse is always the longest side of the triangle formed.
According to the law of conservation of energy, energy can neither be created nor be destroyed but changes from one form to another.
