Question

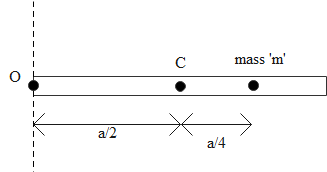
A particle of mass m is attached to a thin uniform rod of length ‘a’ at a distance of $\dfrac{a}{4}$ from the mid point C as shown in the figure. The mass of the rod is ‘4m’. The moment of inertia of the combined system about an axis passing through ‘O’ and perpendicular to the rod is-

Answer 1

The moment of inertia of the combined system of rod and mass m is equal to the sum of moment of inertia due to the rod and the mass. By finding out the expressions of moment of inertia for the rod and the mass, we can find out the required answer.
Formula used:
The moment of inertia of a mass about an axis is given as
$I = M{r^2}$
The moment of inertia of a rod about the axis passing through the one end of the rod is given as
$I = \dfrac{1}{3}M{r^2}$

Complete answer:
We are given that a particle of mass m is attached to a thin uniform rod of length ‘a’ at a distance of $\dfrac{a}{4}$ from the mid-point C. The mass of the rod is given as
$M = 4m$
We need to find out the total moment of inertia of the combined system about an axis passing through ‘O’ and perpendicular to the rod as shown in the figure.
First of all, let us calculate the moment of inertia for the rod. As we know that moment of inertia of the rod about the axis passing through one end of the rod and perpendicular to the rod is given as
${I_{rod}} = \dfrac{1}{3}M{a^2}$
Here M is the mass of the rod and a is the length of the rod. Using the value of mass, we get
${I_{rod}} = \dfrac{1}{3}4m{a^2} = \dfrac{4}{3}m{a^2}$
Now the moment of inertia of the particle of mass m which is at a distance of $\dfrac{{3a}}{4}$ from the axis of rotation is given as
${I_p} = m{\left( {\dfrac{{3a}}{4}} \right)^2} = \dfrac{9}{{16}}m{a^2}$
Now, the total moment of inertia of the combined system is equal to the sum of moment of inertia due to rod and due to the particle of mass m. It is given as
$\begin{aligned} I = \dfrac{4}{3}m{a^2} + \dfrac{9}{{16}}m{a^2} = \dfrac{{64 + 27}}{{3 \times 16}}m{a^2} \\\ = \dfrac{{91}}{{3 \times 16}}m{a^2} = \dfrac{{91}}{{48}}m{a^2} \\\ \end{aligned}$
This is the required answer.

Note:
The moment of inertia is the rotational analogue of the inertia experienced in translational motion. It signifies the resistance faced due to the mass of the object when we try to make the object move in rotational motion.