Question
Question: A particle of mass m is at rest at the origin at time t = 0. It is subjected to a force \(F(t) = F_0...
A particle of mass m is at rest at the origin at time t = 0. It is subjected to a force F(t)=F0e−bt in the x direction. It's speed v(t) is depicted by which of the following curves?
A.
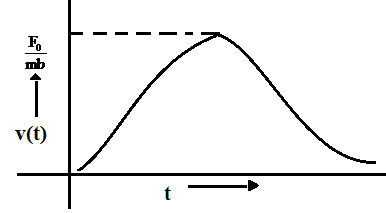
B.
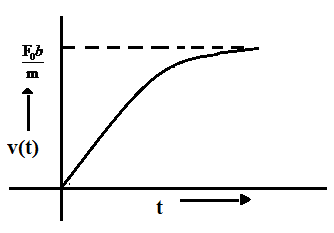
C.
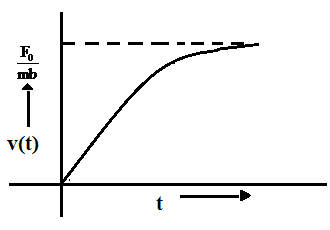
D.
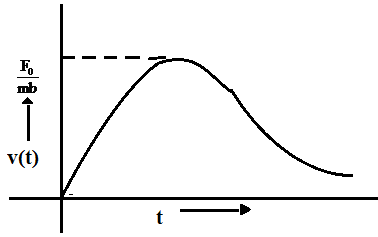
Solution
We are given the expression for force and we know that mass times acceleration is force. By taking integral on both sides on the given expression for force, we will be able to find the velocity expression with respect to time.
Formula used:
Acceleration can be written in terms of velocity as:
a=dtdv.
Complete answer:
The given expression for force is:
F=F0e−bt.
We know that force is just mass times acceleration and using the relation of velocity and acceleration, we may write:
mdtdv=F0e−bt .
We make slight changes in the above expression as:
dv=mF0e−btdt.
Integrating on both sides of this expression keeping the limits t = 0 and t = t.
v(t)−v(0)=mF0∫0te−btdt.
Now, on the LHS we keep v(0) = 0 as is given in the question.
v(t)=(−b)mF0(e−bt)0t
⟹v(t)=−bmF0(e−bt−1)
or we may write,
v(t)=bmF0(1−e−bt).
Now, we require our graph for v(t) to start from 0 as v(0) = 0. On keeping the value t = ∞ we find the graph to saturate at infinity. The peak of the curve must lie at:
v(t)=bmF0(1−0)=bmF0.
This is the velocity that the particle of mass m attains after infinite time.
Therefore, this gives us the required information about the graph.
So, the correct answer is option (B).
Note:
One should not try to make rough guesses for the solution as it will do no good. Though if one is aware of the current equation in the capacitor, one can guess the right answer but to be sure, all the mathematics should be performed and the correct expression should be first obtained. As for the analysis part, we can only tell the behaviour at infinity and zero because of exponential. One must note here that infinity is relative. When we say time is taken as infinity, we are trying to analyse the system after a relatively long time so that all the parameters in the system have settled.
