Question

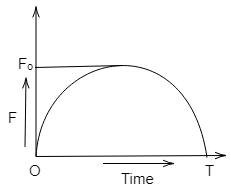
A particle of mass $m$, initially at rest, is acted upon by a variable force $F$ for a brief interval of time $T$. It begins to move with a velocity u after the force stops acting. $F$ is shown in the graph as a function of time. The curve is a semicircle. Then:

$(A)u = \dfrac{{\pi F_o^2}}{{2m}}$
$(B)u = \dfrac{{\pi {T^2}}}{{8m}}$
$(C)u = \dfrac{{\pi {F_o}T}}{{4m}}$
$(D)u = \dfrac{{{F_o}T}}{{2m}}$

Answer 1

In order to solve this question, first we will find the area under the graph from the product of the two quantities on the x and the y axis. Then we will find the area under the graph by calculating the area of the semicircle. Then we will equate these two equations and get the required answer.

Complete step by step solution:
We know that the area under a graph is given by the product of the two quantities which are present on the x and the y axis.
So, in this case the area under the graph will give the value of the product of force and time.
Area under the graph $= F \times t$
On putting the value of force, we get,
Area under the graph $= m \times a \times t$
We also know that the product of acceleration and time gives the value of change in velocity. So, the above expression can be written as,
Area under the graph $= m \times \Delta v......(1)$
In this question,
Mass of the particle $= m$
Final velocity $= u$
Initial velocity $= 0$ (as the particle was initially at rest)
Change in velocity $= u - 0 = u$
On putting these values in equation (1), we get,
Area under the graph $= mu......(2)$
Now, we will calculate the area under the graph by calculating the area of the semicircle.
Area under the graph $= \dfrac{{\pi {r^2}}}{2}......(3)$
On seeing the graph we can see that,
$r = {F_o}......(4)$
On putting the above value in equation (3), we get,
Area under the graph $= \dfrac{{\pi F_o^2}}{2}......(5)$
On equating equation (2) and equation (5), we get,
$mu = \dfrac{{\pi F_o^2}}{2}$
On taking $m$ on the other side, we get,
$u = \dfrac{{\pi F_o^2}}{{2m}}$
So, the correct answer is $(A)u = \dfrac{{\pi F_o^2}}{{2m}}$.

Note:
In this question the area under the force-time graph gave us the product of mass and the change in velocity, which we can say as momentum. Similarly the area under the velocity-time graph gives the displacement and the area under the acceleration-time graph gives the velocity.