Solveeit Logo
Login

Question

Question: A particle of mass \(m\) executes SHM with amplitude \(a\) and frequency \(\nu \). The average kinet...

A particle of mass mm executes SHM with amplitude aa and frequency ν\nu . The average kinetic energy during its motion from the position of equilibrium to the end is
A.14ma2ν2\dfrac{1}{4}m{{a}^{2}}{{\nu }^{2}}
B.4π2ma2ν24{{\pi }^{2}}m{{a}^{2}}{{\nu }^{2}}
C.2π2ma2ν22{{\pi }^{2}}m{{a}^{2}}{{\nu }^{2}}
D.π2ma2ν2{{\pi }^{2}}m{{a}^{2}}{{\nu }^{2}}

Explanation

Solution

We must understand that while giving reference of the position of equilibrium, the problem actually indicates to the mean position of the particle performing simple harmonic motion. We shall find the average kinetic energy using integration and then find the relation of frequency of SHM with one of the quantities included in the formula of the average kinetic energy calculated.

Complete answer:
The time taken by a particle executing simple harmonic motion to travel from its mean position to its extreme position is one-fourth of its total time taken to complete one oscillation, that is, one-fourth of the time period of SHM. Hence, we study the kinetic energy of particles during this time interval, T4\dfrac{T}{4}.

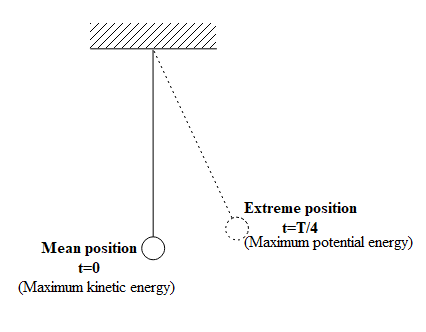
The average kinetic energy during its motion from the mean position to the extreme position is given:
K.E.avg=∫0T412mv2.dt∫0T4dtK.E{{.}_{avg}}=\dfrac{\int\limits_{0}^{\dfrac{T}{4}}{\dfrac{1}{2}m{{v}^{2}}.dt}}{\int\limits_{0}^{\dfrac{T}{4}}{dt}}
Where,
T=T= time period of simple harmonic motion
v=v= velocity of simple harmonic motion
m=m= mass of particle
The velocity of a particle executing simple harmonic motion is given as:
v=aωcos⁡ωtv=a\omega \cos \omega t
Where,
a=a= amplitude of SHM
ω=\omega = angular velocity of SHM
Substituting this value in formula of average kinetic energy, we get
K.E.avg=∫0T412m(aωcos⁡ωt)2.dt∫0T4dtK.E{{.}_{avg}}=\dfrac{\int\limits_{0}^{\dfrac{T}{4}}{\dfrac{1}{2}m{{\left( a\omega \cos \omega t \right)}^{2}}.dt}}{\int\limits_{0}^{\dfrac{T}{4}}{dt}}
Integrating the numerator and denominator separately, we get
K.E.avg=12ma2ω2∫0T4cos⁡2ωt.dtT4K.E{{.}_{avg}}=\dfrac{1}{2}m{{a}^{2}}{{\omega }^{2}}\dfrac{\int\limits_{0}^{\dfrac{T}{4}}{{{\cos }^{2}}\omega t.dt}}{\dfrac{T}{4}}
⇒K.E.avg=14ma2ω2\Rightarrow K.E{{.}_{avg}}=\dfrac{1}{4}m{{a}^{2}}{{\omega }^{2}}
Since T=2πωT=\dfrac{2\pi }{\omega } and frequency, ν=1T\nu =\dfrac{1}{T}, therefore, ω=2πν\omega =2\pi \nu

& \Rightarrow K.E{{.}_{avg}}=\dfrac{1}{4}m{{a}^{2}}{{\left( 2\pi \nu \right)}^{2}} \\\ & \Rightarrow K.E{{.}_{avg}}=\dfrac{1}{4}m{{a}^{2}}\left( 4{{\pi }^{2}}{{\nu }^{2}} \right) \\\ & \Rightarrow K.E{{.}_{avg}}={{\pi }^{2}}m{{a}^{2}}{{\nu }^{2}} \\\ \end{aligned}$$ Therefore, the average kinetic energy is ${{\pi }^{2}}m{{a}^{2}}{{\nu }^{2}}$ **The correct option is (D) ${{\pi }^{2}}m{{a}^{2}}{{\nu }^{2}}$** **Note:** During a simple harmonic motion, a particle consists of both kinetic as well as potential energies. Both of these energies keep fluctuating with every instance of time to keep the total energy constant throughout the motion as the moving particle changes its position. However, the maximum kinetic energy of the particle is at its mean position and the maximum potential energy of particle is at its extreme position