Question

A particle of mass $m$ and charge $q$ is thrown in a region where uniform gravitational fields and electric fields are present. The path of particle is:
(A) May be straight line
(B) May be a circle
(C) May be a parabola
(D) May be a hyperbola

Answer 1

To obtain the path of the particle here we have to consider the two cases one is when there is the angle between gravitational field and electric field is $zero$ and second case with angle between them as $\theta$ .We are supposed to consider two cases as there is no specification of the angle between the two fields in the given question. Forces will be acting on the particle in both the fields.

Complete step by step answer:
Let us consider the two cases
Case I: Angle between gravitational field and electric field be $zero$.
Let the gravitational field and electric field along $x$ - axis and the net acceleration along the axis $y$ - axis because the particle having mass and electrical charge experiences gravitational force and electrical force respectively.
Let ${v_x}$ be the velocity of particle along $x$ direction and ${v_y}$ be the velocity of particle along y direction
Thus the $x$ coordinate of particle is given by $x = {v_x} \times t$
Similarly, $y$ coordinate is given by
$y = {v_y}t + \dfrac{1}{2}{a_{net}}{t^2}$ … $(1)$ (since, along $y$ -axis there is net acceleration which is perpendicular to the fields which would be constant).
$eq(1) \Rightarrow y = \dfrac{x}{{{v_x}}}{v_y} + \dfrac{1}{2}{a_{net}}\left( {\dfrac{{{x^2}}}{{v_x^2}}} \right)$ …………….(as we considered above)
Now observe the equation and put out the constants and the variable terms as follows
${k_1} = \dfrac{{{v_y}}}{{{v_x}}}$ and ${k_2} = \dfrac{{{a_{net}}}}{{2v_x^2}}$
Thus the equation of the motion of the particle is obtained as
$y = {k_1}x + {k_2}{x^2}$
This is nothing but the equation of parabola.
Therefore, the possible trajectory is parabolic.
Case II: Angle between the two fields is $\theta$ . As shown in the figure below:

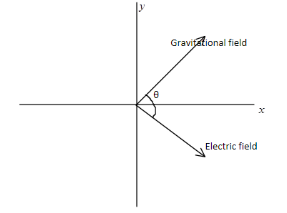
Thus, ${a_x}$ and ${a_y}$ are net accelerations along the both axes respectively,
There we obtain the position of particle about the axes as:
$y = \dfrac{1}{2}{a_y}{t^2}$ $\to {t^2} = 2y{a_y}$
$x = \dfrac{1}{2}{a_x}{t^2}$ $\to {t^2} = 2x{a_x}$
We have obtained the ${t^2}$ from above, now just relating $x$ and $y$ - coordinate, we get
$y = kx$ , here $k$ is a constant
This is the equation of the straight line.
Therefore we can conclude that the path of the particle is straight.
Here, both the options, option A and option C are correct.

Note:
We have not been given the angle between the two fields therefore we have had to consider the two cases and find out the trajectory of the particle. That is why we obtain two solutions and both are correct. The particle is in a straight line or in a parabola.