Question

A particle of mass m and charge q is released from the origin in a region occupied by electric field E and magnetic field B such that $\vec B = - {B_0}\hat j$ ; $\vec E = {E_0}\hat k$ If the speed of the particle as a function of z coordinate is : $v = \sqrt {\dfrac{{xq{E_0}z}}{m}}$. Find x.

Answer 1

Hint: We can use the work-energy theorem to easily find the final speed. Remember the magnetic force doesn’t do work on the system and the work done by electric force is dependent only on the initial and final position.

Complete step by step answer
We know that a charged particle in space would experience a force in the presence of an Electric Field.

If the charge of the particle is $q$ and the electric field is $\vec E$, then the force is given by:
$\overrightarrow {{F_e}} = q\vec E$

Also, If a charged particle of charge $q$ moves with a speed $v$ in a region with a magnetic field $B$,
then the charge experiences the Lorentz force given by the relation:

$\overrightarrow {{F_m}} = q\vec v \times \vec B$

So the electric force is in the direction of the electric field whereas the magnetic force is perpendicular to the plane containing the velocity vector and magnetic field vector.

In this question, the Electric Field is along $+ Z$ direction and the magnetic field is along $- Y$ direction and both have a constant magnitude.

If a particle is released from the origin of a coordinate system, assuming with zero initial velocity, It would not experience any magnetic force in the beginning since $v = 0$.

But as time progresses, the acceleration due to the electric Field would give the particle a velocity along $Z$ direction. The magnetic field would now exert a force in the particle resulting in a complex motion.

So using newton's laws to find the speed would be tedious. We can approach this problem using the work energy theorem.

Let's first find the work done by the magnetic field on the particle.
The work done can be found as:
$dW = \vec F \cdot \overrightarrow {ds}$

but we know that $\vec F$ is perpendicular to the velocity and hence perpendicular to the displacement $dx$
Since the force and displacement are perpendicular to each other always, the magnetic force does not do work on the system.

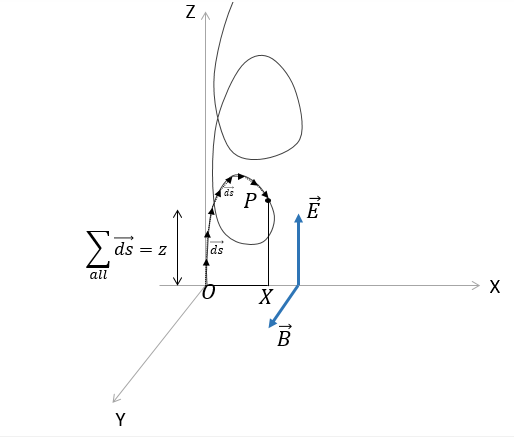
Now let's see the work done by the electric field.
This work is given as:

$dW = \overrightarrow {{F_e}} .\overrightarrow {ds} = q\vec E.\overrightarrow {ds}$
Here we know $\vec E$ and hence $\overrightarrow {{F_e}}$ is always along the $Z$ direction.

For the particle moving approximately as shown in the figure, we can say that

The total work done is the sum : $\sum\limits_{all} {q\vec E \cdot \overrightarrow {ds} }$
If theta is the angle between $\vec E$ and $\overrightarrow {dr}$ , then the sum can be written as

$= \sum\limits_{all} {qE\;ds\;cos\theta }$

Here, E is having a constant magnitude and direction. So we take it outside the summation.
$W = q{E_0}\sum\limits_{all} {\;ds\;cos\theta }$

We see that the Total work done by the electric field is $q{E_0}$ times the sum of all z components of the segments.
From the diagram, we see that adding all these distances would give you the z component of distance moved by the particle.
So we can conclude that the total work done by electric field is ${E_0} \times z$
So the total work done on the particle when it covers a distance is:
work done by magnetic field $+$ work done by electric field

$W = 0 + q{E_0} \times z$

Now we know from the work energy theorem that the Total work done on the particle would be equal to the Change in the kinetic energy of the particle. Here since the particle started at rest, it would be the kinetic energy.

$W = q{E_0} \times z = \dfrac{1}{2}m\;{v^2}$

Now we can easily find the speed at distance z as

${v^2} = \dfrac{{2\;q{E_0}\;z}}{m}$ or $v = \sqrt {\dfrac{{2\;q{E_0}\;z}}{m}}$
So we see that the value of the constant $x$ is 2

Note: The result is true in general for all conservative forces. We could have found the same result more easily. We know the Work done in moving from O to P is independent of the path taken. So by choosing a path like OXP, we could easily see that the total work done by $\vec E$ is
$W = {E_0}\;z\;cos0 + {E_0}\;x\;cos90 = {E_0}\;z$