Question
Question: A particle of mass m and charge \(q\) is attached to a light rod of length \(L\). The rod can rotate...
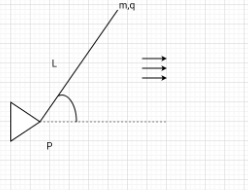
A particle of mass m and charge q is attached to a light rod of length L. The rod can rotate freely in the plane of paper about the other end, which is hinged at P. The entire assembly lies in a uniform electric field E also acting in the plane of the paper as shown. The rod is released from rest when it makes an angle θ with the electric field direction. Determine the speed of the particle when the rod is placed parallel to the electric field.
A) m2qEL(1−cosθ)1/2
B) m2qEL(1−sinθ)1/2
C) 2mqEL(1−cosθ)1/2
D) m2qELcosθ1/2
Solution
If a charge is present in the space, then it will have its effect over its surrounding area. In this area, it can exert forces on all other charges present. This property of the charge is known as the electric field. The electric field is a vector quantity. The direction of the electric field is the direction of the force of a positive test charge.
Complete step by step answer:
Step I:
Let ‘v ’ be the velocity of the particle when it becomes parallel to the electric field. Since the charge q is placed in an electric field E, then the force on the charge will be due to the electric field E. The charge will move due to the force applied by the electric field. This means that the kinetic energy of the charge will be equal to the electric field.
Step II:
Let dW be the amount of work done by the torque to move the rod. When the rod is moved, suppose it makes an angle dθ with the electric field direction.
Therefore work done is given by
dW=qE×Lsinθdθ -----------(i)
where dW is the work done
q is the charge’
E is the electric field
L is the length of the rod
dθ is the angle through which it is displaced
sinθ is the angle it makes with the direction of the electric field.
Step III:
Work done can be calculated by integrating equation (i)
W=∫dW
⇒W=qEL0∫θsinθ
⇒W=qEL[−cosθ]0θ
⇒W=qELcos(θ)−[−cos0]
⇒W=qEL(1−cosθ)
Step IV:
Since the work done is equal to the change in kinetic energy, therefore
K.E.=W ---------(ii)
Formula for K.E.=21mv2
Substitute value of work done and kinetic energy in equation
⇒21mv2=qEL(1−cosθ)
⇒v2=m2qEL(1−cosθ)
⇒v=m2qEL(1−cosθ)1/2
Therefore, Option A is the right answer.
Note:
It is to be remembered that two electric field lines can never intersect with each other. This is because if the electric field lines cross each other, then there will be two different directions of the electric field at that point. This is not possible. Therefore, electric field lines should always be drawn individually.
