Question

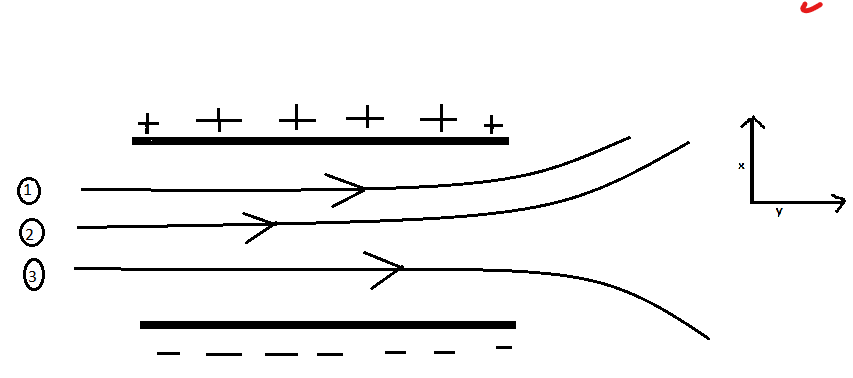
A particle of mass m and charge (-q) enters the region between the two charged plates initially moving along x-axis with speed ${{v}_{x}}$(like particle 1 in Fig.). The length of plate is L and a uniform electric field E is maintained between the plates. Show that the vertical deflection of the particle at the far edge of the plate is ${qE{{L}^{2}}}/{\left( 2mv_{x}^{2} \right)}\;$.
Compare this motion with motion of a projectile in a gravitational field.

Answer 1

- Hint: A negative charged particle moving under the influence of an electric field will get deflected towards the positive plate. The vertical displacement of the charged particle can be calculated by using the equation of motion in y direction.

Complete step-by-step solution -

The particle is moving along the x axis in the presence of uniform electric field E as given in the question.
We have to find the vertical distance covered by the deflected particle along y axis say ‘h’
Time taken by the particle to cover the horizontal distance L with velocity ${{v}_{x}}$ is
$t=\dfrac{L}{{{v}_{x}}}$
Force acting on the particle along y axis due to electric field is,
$F=qE$
Acceleration of the particle along y axis is given by,
$a=\dfrac{F}{m}=\dfrac{qE}{m}$
Now, to calculate the displacement along y axis we will use the equation of motion i.e.
$s=ut+\dfrac{1}{2}a{{t}^{2}}$
Since initial velocity of the particle along y axis is zero, $u=0$
$s=0+\dfrac{1}{2}a{{t}^{2}}$
Substituting the values of acceleration and time from above equations we get,
$s=\dfrac{1}{2}\dfrac{qE}{m}{{\left( \dfrac{L}{{{v}_{x}}} \right)}^{2}}$
Therefore, the vertical deflection of the particle at far edge of the plates is $\dfrac{qE{{L}^{2}}}{2m{{v}_{x}}^{2}}$
The motion of the free charged particle placed in the electric field is analogous to projectile motion as in both the cases there is deflection due to applied forces in a direction perpendicular to the direction of motion of the body/particle.
The vertical displacement for a charged particle in projectile motion is given by
$y=\dfrac{1}{2}a{{t}^{2}}$

Note: Students must remember that the vertical deflection of the charged particle is directly proportional to the ratio of charge and mass of the particle. If $\dfrac{e}{m}$for a particle is large, then the particle will be deflected more and vice versa.