Question

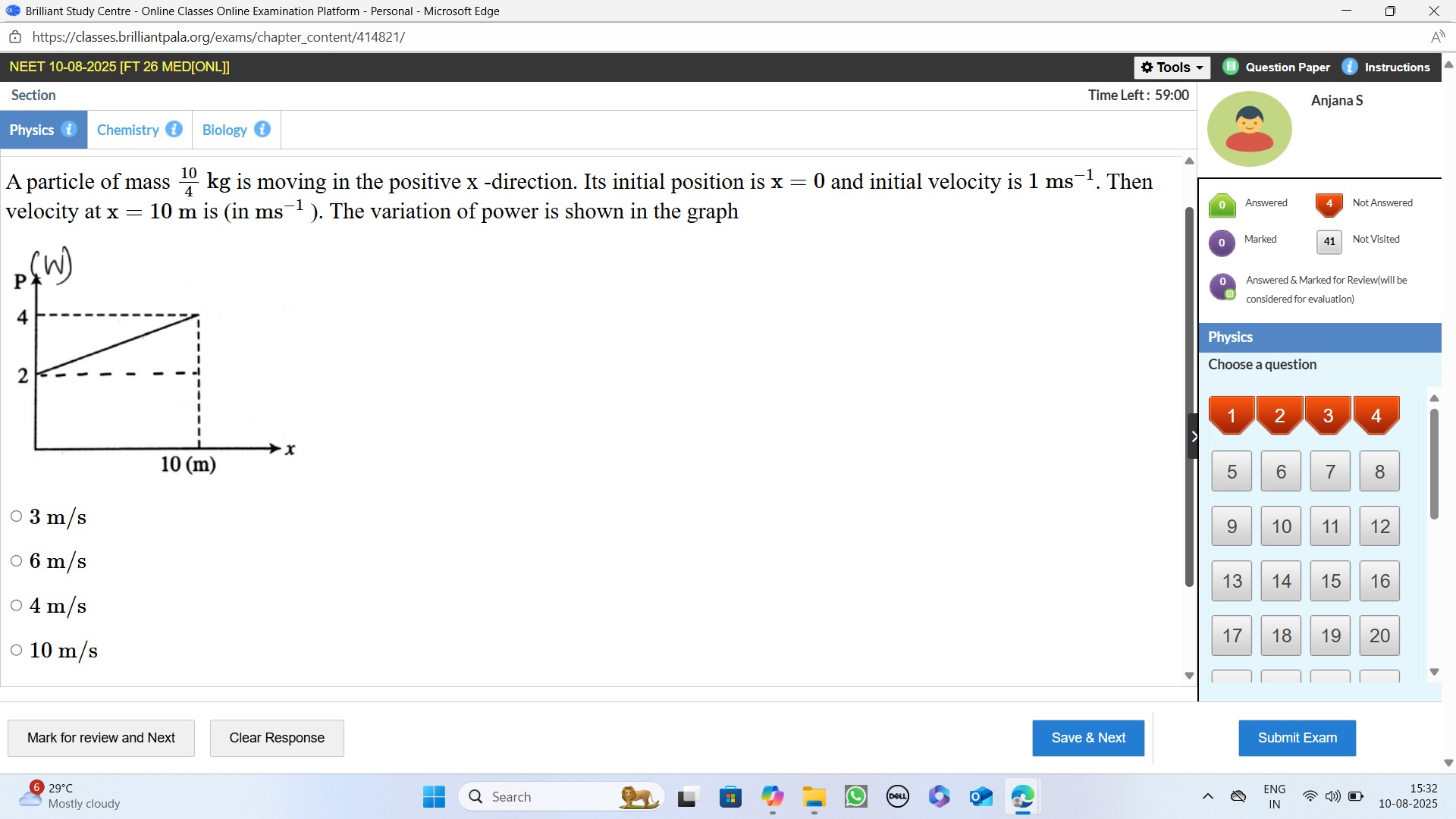
A particle of mass $\frac{10}{4}$ kg is moving in the positive x -direction. Its initial position is x = 0 and initial velocity is 1 $ms^{-1}$. Then velocity at x = 10 m is (in $ms^{-1}$). The variation of power is shown in the graph

• A. 3 m/s
• B. 6 m/s
• C. 4 m/s
• D. 10 m/s

Answer 1

Answer: (A)

3 m/s

Answer 2

The problem asks us to find the final velocity of a particle given its mass, initial conditions, and a graph showing the variation of power with position.

1. Determine the equation for Power P as a function of position x from the graph:
   The graph is a straight line passing through points $(0, 2)$ and $(10, 4)$.
   The slope of the line is $k = \frac{P_2 - P_1}{x_2 - x_1} = \frac{4 - 2}{10 - 0} = \frac{2}{10} = \frac{1}{5}$.
   The P-intercept (value of P at $x=0$) is $2$.
   So, the equation of the line is $P(x) = kx + c = \frac{1}{5}x + 2$.

2. Relate Power to velocity and position:
   Power $P$ is defined as the rate of doing work, $P = \frac{dW}{dt}$.
   According to the Work-Energy Theorem, the work done on a particle is equal to the change in its kinetic energy, $dW = dK$.
   So, $P = \frac{dK}{dt}$.
   Kinetic energy $K = \frac{1}{2}mv^2$.
   Therefore, $P = \frac{d}{dt}\left(\frac{1}{2}mv^2\right) = \frac{1}{2}m \cdot 2v \frac{dv}{dt} = mv \frac{dv}{dt}$.
   To express power in terms of position $x$, we use the chain rule: $\frac{dv}{dt} = \frac{dv}{dx} \frac{dx}{dt} = v \frac{dv}{dx}$.
   Substituting this into the power equation: $P = mv \left(v \frac{dv}{dx}\right) = mv^2 \frac{dv}{dx}$.

3. Set up and solve the differential equation:
   We have $P(x) = \frac{1}{5}x + 2$.
   So, $\frac{1}{5}x + 2 = mv^2 \frac{dv}{dx}$.
   Rearranging for integration: $(\frac{1}{5}x + 2) dx = mv^2 dv$.

Integrate both sides from the initial conditions to the final conditions:
Initial conditions: $x_0 = 0$, $v_0 = 1 \text{ ms}^{-1}$.
Final conditions: $x_f = 10 \text{ m}$, $v_f = v$.

$\int_{0}^{10} \left(\frac{1}{5}x + 2\right) dx = \int_{1}^{v} mv^2 dv$

Left-hand side integral:
$\int_{0}^{10} \left(\frac{1}{5}x + 2\right) dx = \left[\frac{1}{5}\frac{x^2}{2} + 2x\right]_{0}^{10}$
$= \left[\frac{x^2}{10} + 2x\right]_{0}^{10}$
$= \left(\frac{10^2}{10} + 2(10)\right) - \left(\frac{0^2}{10} + 2(0)\right)$
$= (10 + 20) - 0 = 30$.
Alternatively, the integral $\int P dx$ represents the area under the P-x graph. The area is a trapezoid:
Area $= \frac{1}{2} (\text{sum of parallel sides}) \times \text{height} = \frac{1}{2} (P(0) + P(10)) \times (10 - 0)$
Area $= \frac{1}{2} (2 + 4) \times 10 = \frac{1}{2} (6) \times 10 = 3 \times 10 = 30$.

Right-hand side integral:
Given mass $m = \frac{10}{4} \text{ kg} = 2.5 \text{ kg}$.
$\int_{1}^{v} mv^2 dv = m \left[\frac{v^3}{3}\right]_{1}^{v}$
$= m \left(\frac{v^3}{3} - \frac{1^3}{3}\right)$
$= 2.5 \left(\frac{v^3 - 1}{3}\right)$.

4. Equate the integrals and solve for v:
   $30 = 2.5 \left(\frac{v^3 - 1}{3}\right)$
   $30 = \frac{5}{2} \left(\frac{v^3 - 1}{3}\right)$
   $30 = \frac{5(v^3 - 1)}{6}$
   $30 \times 6 = 5(v^3 - 1)$
   $180 = 5(v^3 - 1)$
   $\frac{180}{5} = v^3 - 1$
   $36 = v^3 - 1$
   $v^3 = 36 + 1$
   $v^3 = 37$

Now, we need to find $v = \sqrt[3]{37}$.
Let's check the given options:

• $3^3 = 27$
• $6^3 = 216$
• $4^3 = 64$
• $10^3 = 1000$

None of the options exactly match $v^3 = 37$. The value $\sqrt[3]{37}$ is approximately $3.33$.
There might be a numerical discrepancy in the problem statement or options provided. However, assuming the problem expects one of the options to be correct, and given that $37$ is closest to $27$ (for $v=3$) and $64$ (for $v=4$), none of them are particularly close.

If we strictly follow the calculations, $v = \sqrt[3]{37} \text{ m/s}$. Since this is a multiple choice question, and none of the options are close, let's re-examine if there's any common mistake or if some value could be an approximation.
If the question intends for an integer answer, it implies that $v^3$ should be a perfect cube.
Given the options, $3 \text{ m/s}$ is the closest integer value. However, $3^3 = 27$, not $37$. If the final velocity was meant to be $3 \text{ m/s}$, then $v^3 - 1 = 26$.
Then $30 = \frac{2.5}{3} (26) = \frac{65}{3} \approx 21.67$. This is not 30.

Let's assume there is a typo in the mass value or initial velocity.
If $v=3 \text{ m/s}$ was the answer, then $v^3 = 27$.
Then $30 = \frac{m}{3}(27-1) = \frac{26m}{3}$.
$m = \frac{90}{26} = \frac{45}{13} \approx 3.46 \text{ kg}$. This is not $2.5 \text{ kg}$.

If the question meant to give a perfect cube result, then $v^3$ should be $27$ or $64$.
If $v^3=27$, then $v=3 \text{ m/s}$.
If $v^3=64$, then $v=4 \text{ m/s}$.

Let's re-check the graph values. P starts at 2 and ends at 4 for x from 0 to 10. This seems clear.
The mass is $10/4 = 2.5$ kg. This is clear.
Initial velocity is 1 m/s. This is clear.

Given the options, it's possible the question expects us to choose the closest integer, but that's not standard practice without specific instructions.
However, in competitive exams, sometimes values are slightly off and the closest option is chosen.
$3.33^3 \approx 37$.
$3^3 = 27$
$4^3 = 64$
$37$ is closer to $27$ than $64$. The distance $|37-27|=10$, while $|37-64|=27$.
So $v=3$ would be the "closest" integer option if an integer answer is expected.

Let's consider if the question meant $P = mv \frac{dv}{dx}$ instead of $P = mv^2 \frac{dv}{dx}$.
No, $P = Fv = ma v = m (v \frac{dv}{dx}) v = mv^2 \frac{dv}{dx}$ is correct.

Given the options, and assuming there is no calculation error, there might be a slight numerical inaccuracy in the problem's design. If we must choose an option, $v=3$ is the closest integer value to $\sqrt[3]{37}$.

Final check:
Mass $m = 2.5 \text{ kg}$.
Initial velocity $v_0 = 1 \text{ m/s}$.
Area under P-x graph from $x=0$ to $x=10$ is $30 \text{ J}$.
This area equals $\frac{m}{3}(v_f^3 - v_0^3)$.
$30 = \frac{2.5}{3}(v_f^3 - 1^3)$
$90 = 2.5 (v_f^3 - 1)$
$36 = v_f^3 - 1$
$v_f^3 = 37$.

The result $v_f = \sqrt[3]{37} \text{ m/s}$ is correct based on the problem statement. Since none of the options are $\sqrt[3]{37}$, there is a mismatch. If I have to pick the closest one, $3^3=27$ and $4^3=64$. $37-27=10$ and $64-37=27$. So $3$ is the closest integer for $v$.

Let's assume the question expects the answer to be $3 \text{ m/s}$ and see what value of mass would lead to this.
$30 = \frac{m}{3}(3^3 - 1^3) = \frac{m}{3}(27-1) = \frac{26m}{3}$.
$m = \frac{90}{26} = \frac{45}{13} \approx 3.46 \text{ kg}$.
This is different from the given mass of $2.5 \text{ kg}$.

Let's assume the question expects the answer to be $4 \text{ m/s}$.
$30 = \frac{m}{3}(4^3 - 1^3) = \frac{m}{3}(64-1) = \frac{63m}{3} = 21m$.
$m = \frac{30}{21} = \frac{10}{7} \approx 1.43 \text{ kg}$.
This is also different from the given mass of $2.5 \text{ kg}$.

Since the calculation leads to $v^3 = 37$, and this is not among the options, there is an error in the question's values or options. However, if forced to choose, the closest integer value of $v$ such that $v^3$ is near $37$ is $v=3$.

Given the context of multiple-choice questions, sometimes they are designed such that the answer is one of the options, even if it requires a slight approximation or a rounding.
If we consider $v \approx 3.33$, then $3$ is the closest integer answer among the choices.