Question

A particle of mass $80$ units is moving with uniform speed $v = 4\sqrt 2$units in $xy$plane, along a line$y = x + 5$. The magnitude of the angular momentum of the particle about the origin is.
$(A)1600{\text{units}}$
$(B)160\sqrt 2 {\text{units}}$
$(C)152\sqrt 2 {\text{units}}$
$(D)16\sqrt 2 {\text{units}}$

Answer 1

The formula of the angular momentum of the particle has to be used to solve the problem. The formula gives the relationship between the mass of the particle and velocity speed of the particle and the radius of the circular path of the particle. Then determine the perpendicular distance of the line of motion of the particle and also substitute the values into the formula for the angular momentum of the particle.

Complete step-by-step solution:
The angular momentum of an object moving with some linear speed is given by
$L = mv{r_p}$
Here,
$m =$Mass$= 80$units
$\nu =$Speed$= 4\sqrt 2$
{r_p}$$$$ = The perpendicular distance from reference to the momentum
The graph for the motion of the particle along the given line as follows:

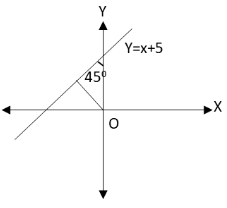
The angle made by the line of motion of the particle with $x$and$y$axis is${45^ \circ }$.
Perpendicular distance of origin from a given line $y = x + 5$ is given by
${r_p} = 5\cos {45^ \circ } = \dfrac{5}{{\sqrt 2 }}$

Now, the angular momentum is
$L = 80 \times 4\sqrt 2 \times \dfrac{5}{{\sqrt 2 }}$
$L = 1600$
Therefore, the magnitude of angular momentum of the particle about the origin is$1600$units.

Note: The rotational momentum of a rotating body or system is measured by a vector quantity.
The product of the angular velocity of the body with respect to the rotation axis, and which is directed along the rotation axis.
The law of angular momentum states that when no external torque acts on an object, no change of angular momentum will occur.