Question

A particle of mass 80 units is moving with a uniform speed $v = 4\sqrt 2 \,{\text{units}}$ in XY plane, along a line $y = x + 5$. The magnitude of the angular momentum of the particle about the origin is:
A. $1600\,{\text{units}}$
B. $160\sqrt 2 \,{\text{units}}$
C. $152\sqrt 2 \,{\text{units}}$
D. $16\sqrt 2 \,{\text{units}}$

Answer 1

Use the formula for angular momentum of the particle. This formula gives the relation between mass of particle, velocity of particle and radius of the circular path of particle. Determine the perpendicular distance of the line of motion of the particle and substitute it in the formula for angular momentum of the particle.

Formula used:
The angular momentum $L$ of a particle is given by
$L = mvr$ …… (1)
Here, $m$ is the mass of the particle, $v$ is velocity of the particle and $r$ is radius of circular path of the particle.

Complete step by step answer:
We have given that the mass of the particle is 80 units.
$m = 80\,{\text{units}}$
The speed of the particle is $4\sqrt 2 \,{\text{units}}$.
$v = 4\sqrt 2 \,{\text{units}}$
The particle is moving along the line $y = x + 5$.
The graph for the motion of particle along the given line is as follows:

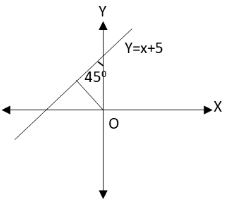
The angle made by the line of motion of the particle with the X and Y axis is $45^\circ$. We have asked the angular momentum of the particle about the origin.
Rewrite the equation (1) for angular momentum of the particle about the origin.
$L = mv{r_p}$ …… (2)
Here, ${r_p}$ is the perpendicular distance of a particle from origin.
The perpendicular distance of particle from origin is given by
${r_p} = 5\cos 45^\circ$
${r_p} = \dfrac{5}{{\sqrt 2 }}\,{\text{units}}$
Substitute $80\,{\text{units}}$ for $m$, $4\sqrt 2 \,{\text{units}}$ for $v$ and $\dfrac{5}{{\sqrt 2 }}\,{\text{units}}$ for ${r_p}$ in equation (2).
$L = \left( {80\,{\text{units}}} \right)\left( {4\sqrt 2 \,{\text{units}}} \right)\left( {\dfrac{5}{{\sqrt 2 }}\,{\text{units}}} \right)$
$\therefore L = 1600\,{\text{units}}$
Therefore, the angular momentum of the particle about origin is $1600\,{\text{units}}$.

Hence, the correct option is A.

Note: The students should not forget that we have asked to determine the angular momentum of the particle about origin. Therefore, the students should not forget to use the perpendicular distance of the line of motion of the particle from the origin. If the perpendicular distance is not used then the final answer will be incorrect.