Question

A particle of mass 5kg is moving with a uniform speed $3\sqrt 2$ in the XOY plane along the line $Y = X + 4$. The magnitude of its angular momentum about the origin is:
A.$40\,{\text{units}}$
B.$60\,{\text{units}}$
C.0
D.$40\sqrt 2 \,{\text{units}}$

Answer 1

Use the formula for the angular momentum of the particle. This formula gives the relation between the mass of the particle, velocity of the particle, position of the particle and the angle between the velocity vector and position vector of the particle.

Formula used:
The expression for the angular momentum of the particle is
$L = mvr\sin \theta$ …… (1)
Here, $L$ is the angular momentum of the particle, $m$ is the mass of the particle, $v$ is the velocity of the particle, $r$ is the position of the particle and $\theta$ is the angle between the velocity vector and position vector of the particle.

Complete step by step answer:
The mass of the particle is $5\,{\text{kg}}$ and its speed is $3\sqrt 2$.
$m = 5\,{\text{kg}}$
$v = 3\sqrt 2 \,{\text{units}}$

The equation representing the position vector of the particle is $Y = X + 4$.

The graph representing the direction of motion of the particle is as follows:

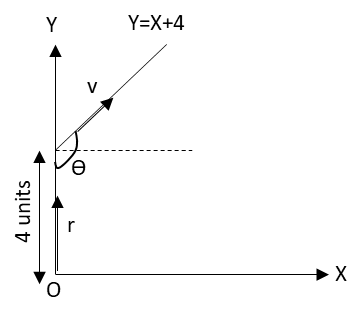
In the above figure, the graph showing the direction of motion of the particle is shown. $4\,{\text{units}}$ is the distance of origin from the particle and $\theta$ is the angle between the position vector from the origin and the velocity vector.
$r = 4\,{\text{units}}$

The angle between the horizontal X axis and velocity vector is $45^\circ$ and the angle between the position vector and the horizontal is $90^\circ$.

Hence, the angle between the velocity vector of particle and the position vector from the origin is
$\theta = 45^\circ + 90^\circ$
$\Rightarrow \theta = 180^\circ - 45^\circ$

We can determine the angular momentum of the particle from the origin using equation (1).

Substitute $5\,{\text{kg}}$ for $m$, for $v$, $4\,{\text{units}}$ for $r$ and $180^\circ - 45^\circ$ for $\theta$ in equation (1).
$L = \left( {5\,{\text{kg}}} \right)\left( {3\sqrt 2 \,{\text{units}}} \right)\left( {4\,{\text{units}}} \right)\sin \left( {180^\circ - 45^\circ } \right)$
$\Rightarrow L = \left( {5\,{\text{kg}}} \right)\left( {3\sqrt 2 \,{\text{units}}} \right)\left( {4\,{\text{units}}} \right)\sin 45^\circ$
$\Rightarrow L = \left( {5\,{\text{kg}}} \right)\left( {3\sqrt 2 \,{\text{units}}} \right)\left( {4\,{\text{units}}} \right)\dfrac{1}{{\sqrt 2 }}$
$\Rightarrow L = 60\,{\text{units}}$

Therefore, the angular momentum of the particle about the origin is $60\,{\text{units}}$.

Hence, the correct option is B.

Note:
One can also determine the perpendicular distance between the origin and the velocity instead of measuring sine of the angle between the velocity vector and the position vector from the origin. Also, the students may get confused about how $\sin \left( {180^\circ - 45^\circ } \right)$ is directly replaced by $\sin 45^\circ$. But these two quantities have the same value.