Question

A particle of mass $4m$ at rest, explodes into three fragments. Two of the fragments each of mass $m$ are found to move with a speed $V$ in mutually perpendicular directions. The total energy released in the explosion is:
A) $2m{V^2}$
B) $\dfrac{1}{2}m{V^2}$
C) $m{V^2}$
D) $\dfrac{3}{2}m{V^2}$

Answer 1

We can easily solve this question by using the law of conservation of momentum and then calculating the energy of the particles after explosion. For that we have to calculate the mass of the third particle and the velocity of that particle. After that we can use the formulae of kinetic energy to calculate the energy after the explosion.

Formula Used:
Momentum = $m \times v$
Where $m$ is mass and $v$ is the velocity.
Law of conservation of momentum
Initial momentum = final momentum
Where initial momentum is the momentum of the particles before explosion and final momentum momentum is the momentum of the particles after explosion.
$KE = \dfrac{1}{2}m{v^2}$
Where $KE$ is the kinetic energy of the particle, $m$ is mass and $v$ is the velocity.

Complete step by step answer:
In the question, the mass of the particle before explosion is given to be $4m$. After the explosion, the same particles break down into three pieces.

The masses of two out of three particles after explosion are given as $m$ and $m$. According to the law of conservation of mass, mass will be constant before and after will be the same. Hence the mass of the third particle will be,
$\Rightarrow mass = 4m - \left( {m + m} \right) = 2m$

To calculate the energy of the energy released, we have to calculate the velocity of the third particle.
In the question it’s given that the velocities of two particles are mutually perpendicular with each other magnitude $V$. Suppose after Collision, particle one moves horizontally and particle two moves vertically.
Let the
${V_1} = V$ $\hat i$ and ${V_2} = V$ $\hat j$
Where ${V_1}$ is the velocity of particle one and ${V_2}$ is the velocity of particle two.
Now,
Using Law of Conservation of momentum, we get
$\Rightarrow 4mu = mV \hat i + mV \hat j + 2m\vec V$
Here $u$ is the initial velocity of the system which is zero.
$\Rightarrow {\vec V_3} = - \dfrac{V}{2}\left( {\hat i + \hat j} \right)$
Negative sign shows that ${V_3}$ moves in the opposite direction of particle one and particle two.

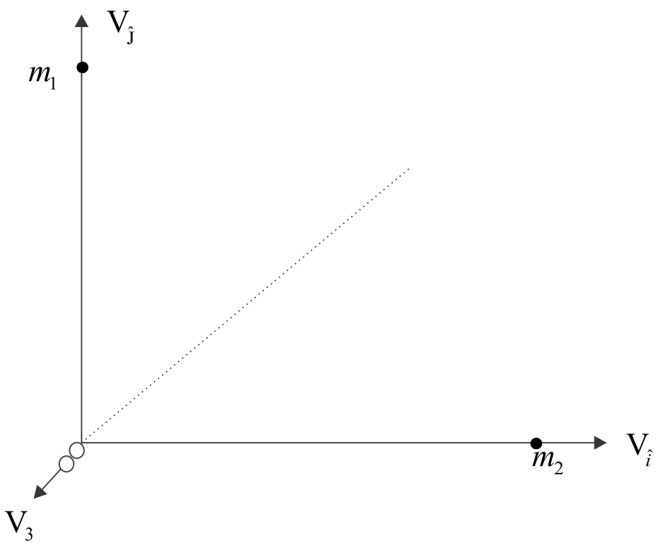
From the diagram, it is clear that the velocity of particle three will be equal in the magnitude of the resultant of velocities of particle one and two, but in the opposite direction. Hence the magnitude of velocity of the third particle will be
$|\mathop {{V_3}}\limits^ \to | = \dfrac{V}{2} \times \sqrt 2 = \dfrac{V}{{\sqrt 2 }}$
Therefore, total Energy released is equal to Sum of kinetic Energy of three particles.

After substituting the values of velocity and mass of all the particles, the total energy becomes,
$E(total) = \dfrac{1}{2}m{V^2} + \dfrac{1}{2}m{V^2} + \dfrac{1}{2}(2m){\left( {\dfrac{V}{{\sqrt 2 }}} \right)^2}$
$\Rightarrow E\left( {total} \right) = \dfrac{3}{2}m{V^2}$

Hence, Option (D) is the correct answer.

Note: While calculating mass and velocity for particles, it is very important to check the initial and final conditions of the system. We can use the formulae of conservation of momentum only if it clearly gives us details of all the particles before any collision or explosion and after any collision or explosion.