Question

A particle of mass $4\;m$ is projected from the ground at some angle with the horizontal. Its horizontal range is $R$. At the highest point its path breaks into two pieces of masses $m$ and $3\;m$ respectively, such that the smaller mass comes to rest. The larger mass finally falls at a distance $x$ from the point of projection, where $x$ is equal to:
A. $\dfrac{2R}{3}$
B. $\dfrac{7R}{6}$
C. $\dfrac{5R}{4}$
D. none of these

Answer 1

A body when projected at an inclination from the ground, I said to experience projectile motion. Then the path followed by the body is called the ballistic trajectory, which is a curved parabolic path. Here, we need to calculate the distance covered by the body after breaking into two pieces.
Formula used:
$mv=constant$
$v=\dfrac{x}{t}$

Complete answer:
Let $u$ be the initial velocity of the body which is projected at an angle $\theta$ from the horizontal. Then the initial velocity $u$ can be resolved into two components along the x and y axis respectively .Let $H$ and $R$ be the maximum distances along the x and y-axis respectively, during the time of flight $T$ Consider the figure as shown below:

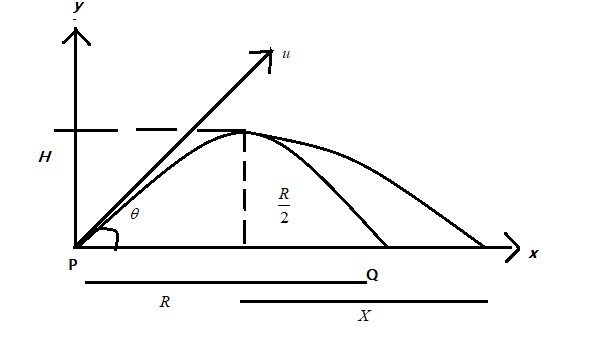
We know that the distance covered by the body along the x and y-axis respectively is given as, $R$ and $H$ which is the maximum horizontal range and maximum height attained by the object.
Then , we have $R=2ucos \theta t$
The maximum height $H$ is attained at $\dfrac{R}{2}$
Here, the $4\;m$ body breaks at $H$ into $3\;m$ and $m$. Also, after breaking the velocity of the $m$ particle becomes $0$. And let the velocity of the $3\;m$ be $v$.
From the conservation of momentum, we can say that the momentum of the body before breaking is equal to the sum of the momentum of the particles after braking.
$\implies 4mucos\theta=3mv+m0$
$\implies v=\dfrac{4}{3}ucos\theta$
Let the distance covered by the $3\;m$ body be $x$ in time $t$, then we have, $x=vt$
$\implies x=\dfrac{4}{3}ucos\theta t$
Replacing $ucos\theta t$ as $\dfrac{R}{2}$, we get
$\implies x=\dfrac{4}{3}\times \dfrac{R}{2}$
$\implies x=\dfrac{4R}{6}$
Then the total distance covered by the body is given as $D=\dfrac{R}{2}+x$
$\implies D=\dfrac{R}{2}\left(1+\dfrac{4}{3}\right)$
$\implies D=\dfrac{7R}{6}$

Thus the correct answer is option B. $\dfrac{7R}{6}$

Note:
When the object is on the air, the only force acting on it is the force due to gravity, which pulls the object back to the surface at the speed of acceleration due to gravity. Note that the range of the projected body is generally greater than the distance covered by it when dropped from the same height.