Question

A particle of mass $2m$ is projected at an angle of $30^\circ$with the horizontal with a velocity of$40m/s$. After $1s$ explosion takes place and the particle is broken into two equal pieces. As a result of the explosion, one part comes to rest. The maximum height from the ground attained by the other part is $(g = 10m/{s^2})$
(A) $50m$
(B) $25m$
(C) $40m$
(D) $35m$

Answer 1

Hint In a projectile motion, the particle follows a parabolic path. By$1s$, it has already traveled, some vertical as well as horizontal distance. After it explodes, the second part shoots up in the air again, following a projectile path. The velocity of the particle can be determined by using the law for conservation of linear momentum. Both the heights are then added to give the maximum height.
Formula used:
$T = \dfrac{{2u\sin \theta }}{g}$
${V^2} = {U^2} + 2as$
$s = Ut + \dfrac{1}{2}a{t^2}$
$V = U + at$

Complete Step By Step Solution

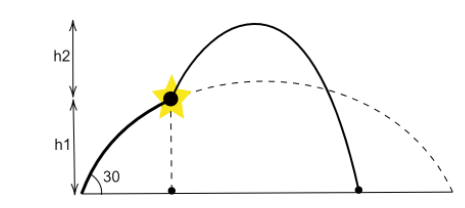
It is given in the question that,
Angle of projection of the particle, $\theta = 30^\circ$
Initial velocity$u = 40m/s$
The horizontal component of velocity, ${u_x} = u\cos \theta$
${u_x} = 40\cos 30^\circ$
${\vec u_x} = 20\sqrt 3 \hat i$ \left\\{ {\cos 30^\circ = \dfrac{{\sqrt 3 }}{2}} \right\\}
The vertical component of velocity, ${u_y} = u\sin \theta$
${u_y} = 40\sin 30^\circ$
${\vec u_y} = 20\hat j$ \left\\{ {\sin 30^\circ = \dfrac{1}{2}} \right\\}
The time of flight of the original projectile would have been,
$T = \dfrac{{2u\sin \theta }}{g}$
$T = \dfrac{{2 \times 40 \times \dfrac{1}{2}}}{{10}}$
$T = 4\sec$
We know that initial velocity,
$\vec u = 20\sqrt 3 \hat i + 20\hat j$
Using the first equation of motion,
$V = U + at$
The acceleration is $a = g = - 10m/{s^2}$ acting downwards.
We have the velocity after $1s$,
$\vec v = \left( {20\sqrt 3 \hat i + 20\hat j} \right) + \left( { - 10\hat j} \right) \times 1$
$\vec v = 20\sqrt 3 \hat i + 10\hat j$
Initial mass of the particle ${m_i} = 2m$
It is said that after the explosion it divides into two equal parts,
The mass of the particle after explosion, ${m_f} = m + m$
Applying the law of conservation of momentum to the particle, we have-
$2m\vec v = m{\vec v_1} + m{\vec v_2}$
$2m\left( {20\sqrt 3 \hat i + 10\hat j} \right) = 0 \times m + mv'$
$v' = 40\sqrt 3 \hat i + 20\hat j$
Here, $v'$is the velocity with which the second part of the particle moves after the explosion. The force of gravity acts on it, therefore maximum height covered by this particle is given by the third equation of motion-
${V^2} = {U^2} + 2as$
Here, $V = 0$ ,$U = {\vec v_y} = 20\hat j$,$a = - 10$,$s = {h_2}$
By putting these values we have,
$0 = 400 + 2( - 10){h_2}$
$400 = 20{h_2}$
${h_2} = 20$
The height traveled by the particle after the explosion is $20m$.
But before explosion, the particle has already covered a height, ${h_1}$
Using the second equation of motion,
$s = Ut + \dfrac{1}{2}a{t^2}$
Keeping values of $s = {h_1},a = - 10,U = u\sin \theta = 20\hat j,t = 1$
We can write-
${h_1} = 20 \times 1 + \dfrac{1}{2} \times ( - 10) \times {1^2}$
${h_1} = 20 - 5 = 15$
The total height covered by the particle is,
$H = {h_1} + {h_2}$
$H = 15 + 20 = 35$
The maximum height attained by the particle from ground is$35m$.

Option (4) is correct.

Note It should be kept in mind that to calculate the maximum height, only the vertical components of all the velocities are taken in calculation. However, for the equations involving the law of conservation of momentum, both components of velocity are used.