Question

A particle of mass 200 g, is whirled into a vertical circle of radius 80 cm using a massless string. The speed of the particle when the string makes an angle $60^\circ$ with the vertical line is $1.5\,{\text{m}}{{\text{s}}^{ - {\text{1}}}}$. The tension in the string at this position is:
A. 1 N
B. 1.56 N
C. 2 N
D. 3 N

Answer 1

Apply Newton’s second law to the motion of the particle at this position and balance the forces. Use the expression for centripetal force which balances the tension in the string. If the tension has negative value, it means the tension is along the negative direction of the preferred axis.

Formula used:
Centripetal force, ${F_C} = \dfrac{{m{v^2}}}{r}$
Here, m is the mass, v is the velocity and r is the radius of circular motion.

Complete step by step solution:
We have given the mass of the particle, $m = 200\,g = 0.2\,kg$, the radius of the circular motion, $r = 80\,cm = 0.8\,m$, the velocity of the particle, $v = 1.5\,m/s$ and angle made by the string with vertical $\theta = 60^\circ$.
When we whirl a particle in circular motion, only three forces act on the particle: weight of the particle, tension in the string and centripetal force.
We can draw the forces acting on the particle as follows,

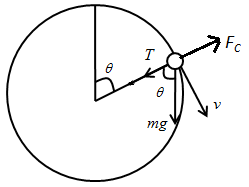
In the above figure, ${F_C}$ is the centripetal force, T is the tension and mg is the weight of the particle.
The free body diagram can be drawn as shown in the figure below.

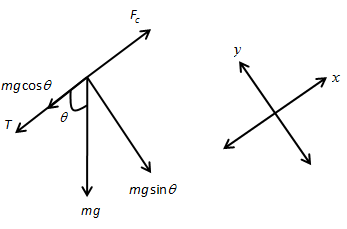
Applying Newton’s second law of motion in the x-direction, we get,
$- T - mg\cos \theta = {F_C}$
$\Rightarrow T = - {F_C} - mg\cos \theta$ …… (1)
We have centripetal force is given as,
${F_C} = \dfrac{{m{v^2}}}{r}$
Using the above equation in (1), we get,
$T = - \dfrac{{m{v^2}}}{r} - mg\cos \theta$
$\Rightarrow T = - m\left( {\dfrac{{{v^2}}}{r} + g\cos \theta } \right)$
Substituting $m = 0.2\,kg$, $r = 0.8\,m$, $v = 1.5\,m/s$, $g = 10\,m/{s^2}$ and $\theta = 60^\circ$ in the above equation, we get,
$T = - \left( {0.2} \right)\left( {\dfrac{{{{\left( {1.5} \right)}^2}}}{{0.8}} + \left( {10} \right)\cos \left( {60^\circ } \right)} \right)$
$\Rightarrow T = - 1.56\,N$
The negative sign represents the tension in the string along the negative x-axis.

So, the correct answer is “Option B”.

Note:
In the circular motion, the tension in the string balances the centrifugal force on the particle. Therefore, the directions of these two should be opposite to each other and not in the same direction towards the centre. While applying Newton’s second law, make sure that the acceleration is zero along this direction. In our solution, the particle does not move along the x-axis.