Question
Question: A particle of mass 200 g is attached to an ideal string of length 1.30 m whose upper end is fixed to...
A particle of mass 200 g is attached to an ideal string of length 1.30 m whose upper end is fixed to the ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g=10m/s2)
& (1)\,\dfrac{13}{6}N \\\ & (2)\,\dfrac{11}{6}N \\\ & (3)\,\dfrac{26}{5}N \\\ & (4)\,Zero \\\ \end{aligned}$$Solution
We will be equating the normal force to the vertical component of the string to find the value of the tension in the string, as, the vertical component of the string represents the tension in the string.
Formula used:
T=cosθmg
Complete step by step solution:
The particle attached to an ideal string with upper end fixed revolving in a horizontal circle forms a cone of radius equal to the radius of the circle and the height being equal to the length of the string.
From the given information, we have the data as follows.
The mass of the particle, m=200g
⇒m=0.2kg
The length of the string, l=1.30m
The radius of the circle, r=50m
r=0.5m
The acceleration due to gravity, g=10m/s2
Consider a figure that represents the particle attached to an ideal string with upper end fixed revolving in a horizontal circle.
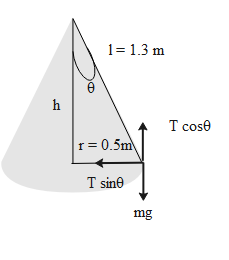
The tension in the string is given by the vertical component. Therefore, the tension in the string is,
Tcosθ=mg
Because the vertical component of the tension equals the normal force.
Thus, the tension in the string is,
T=cosθmg
Now, we will compute the value of the cosine angle.
The cosine angle is given by the formula as follows.
