Solveeit Logo
Login

Question

Question: A particle of mass \(2\times {{10}^{-5}}Kg\) moves horizontally between two horizontal plates of a c...

A particle of mass 2×10−5Kg2\times {{10}^{-5}}Kg moves horizontally between two horizontal plates of a charged parallel plate capacitor between which there is an electric field of 200 N/C acting upward. A magnetic induction of 2.0 T is applied at right angles to the electric field in a direction normal to both B and v. If g is 9.8m/s29.8m/{{s}^{2}} and the charge on the particle is 10−6C{{10}^{-6}}C, then find the velocity of charge particle so that it continues to move horizontally.
A: 2m/s
B: 20m/s
C: 0.2 m/s
D:100m/s

Explanation

Solution

This comes under the application of Lorentz force that is the force which is generated on a charged particle due to the presence of an electric field and a magnetic field. We are given a similar condition here. We can approach this question by keeping the principle of Lorentz force in our minds.

Complete step by step answer:
We are given that
Mass of the particle is 2×10−5Kg2\times {{10}^{-5}}Kg
Upward electric field acting on the particle is 200N/C
Magnetic induction is 2.0 T
Charge on the particle is 10−6C{{10}^{-6}}C
Acceleration due gravity is 9.8m/s29.8m/{{s}^{2}}
We have to find the velocity of the charged particle to maintain the horizontal motion.

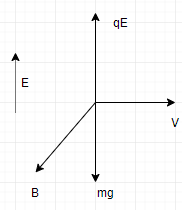
The electric force acting on the particle is F=qE=10−6×200=2×10−4NF=qE={{10}^{-6}}\times 200=2\times {{10}^{-4}}N
The weight that acts downwards is W=mg=2×10−5×9.8=1.96×10−4W=mg=2\times {{10}^{-5}}\times 9.8=1.96\times {{10}^{-4}}
This implies that F>WF>W. Hence to make the net force zero, F has to act downwards.
F=(2−1.96)×10−4=4×10−6   ⟹  10−6×2×v=4×10−6 ∴v=2m/s  F=(2-1.96)\times {{10}^{-4}}=4\times {{10}^{-6}} \\\ \implies {{10}^{-6}}\times 2\times v=4\times {{10}^{-6}} \\\ \therefore v=2m/s \\\

So, the correct answer is “Option A”.

Note:
The Lorenz force is best explained using the right hand rule, where the middle finger represents the force, index finger represents the magnetic field and as a result the thumb represents the direction of the current. This method helps the students to find the directions in a simpler way.