Solveeit Logo
Login

Question

Question: A particle of mass \(2\,kg\) is initially at rest. A force acts on it whose magnitude changes with t...

A particle of mass 2 kg2\,kg is initially at rest. A force acts on it whose magnitude changes with time. The force time graph is shown below. The velocity of the particle after 10 s10\,s is

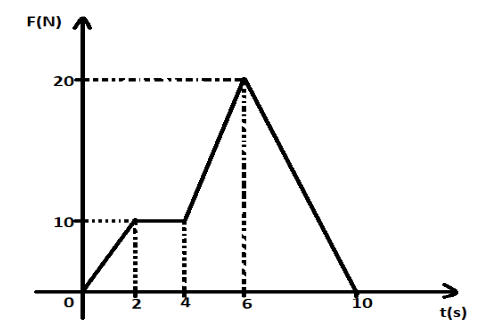
A. 20 m s−120\,m\,{s^{ - 1}}
B. 50 m s−150\,m\,{s^{ - 1}}
C. 75 m s−175\,m\,{s^{ - 1}}
D. 26 m s−126\,m\,{s^{ - 1}}

Explanation

Solution

This question can be evaluated using Newton’s second law of motion in the correct manner. Some basic mathematical approach in the right place will give the correct solution. Most important part is that the area under the slope of force – time graph gives impulse.

Complete step by step answer:

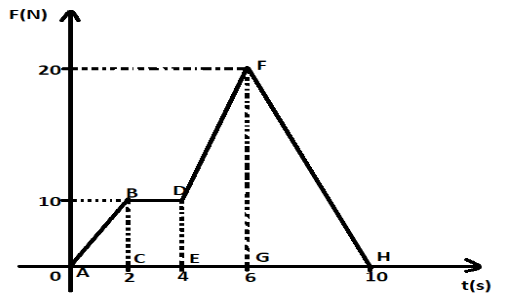
The given graph is of force against time, so area under the slope of this graph will give value of force product of time as,
Force ×\times Time
According to Newton’s second law of motion,
F=ma=mΔvΔtF = ma = m\dfrac{{\Delta v}}{{\Delta t}}
Where, FF = Force; mm = mass; aa = acceleration;
Δv\Delta v = change in velocity; Δt\Delta t = change in time
Above equation can be written as,
F×Δt=m×ΔvF \times \Delta t = m \times \Delta v ……… (i)
Where,
F×ΔtF \times \Delta t represent area under the slope of force-time graph
m×Δvm \times \Delta v represent change in impulse of body
Equation (i) can be written for 10 sec time as,
F×(t10−t0)=m×(v−u)F \times \left( {{t_{10}} - {t_0}} \right) = m \times \left( {v - u} \right)

According to the question body starts initially from rest i.e. initial velocity at t = 0 is given to be u = 0.
Area under slope up to 10 sec time =F×t10=m×v = F \times {t_{10}} = m \times v
Area under slope = mv = Area of triangle ABC and FGH + Area of rectangle BCDE + Area of trapezium DEFG.
Applying formulas and values of areas from graph,
mv=(12×2×10)+(12×4×20)+(2×10)+(12×2×(10+20))mv = \left( {\dfrac{1}{2} \times 2 \times 10} \right) + \left( {\dfrac{1}{2} \times 4 \times 20} \right) + \left( {2 \times 10} \right) + \left( {\dfrac{1}{2} \times 2 \times \left( {10 + 20} \right)} \right)
Evaluating above equation will give,
v=50 m s−1v = 50\,m\,{s^{ - 1}}
The velocity of the particle after 10 sec is 50 m s−150\,m\,{s^{ - 1}}.

Hence, the correct answer is option B.

Note: Area under the slope graph always gives the product of term on Y-axis with term on X-axis. Area under the slope is an integrated term while if we calculate the slope of the graph i.e. value of slope at any point, will give the differentiated term.