Question

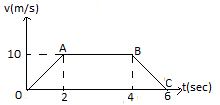
A particle of mass $1kg$ is moved under the action of force and the velocity-time graph of the particle is shown in figure. Work done by the force from $t = 0$ to $t = 6\sec$ is?

Answer 1

Hint We know according to the work energy theorem, the work done by resultant forces on a particle is equal to change in its kinetic energy.
i.e. $W = {K_f} - {K_i}$
where
$\Rightarrow$ ${K_f}$ is final kinetic energy
$\Rightarrow$ ${K_i}$ is initial kinetic energy.
We will use the above concept to find the work done under a given velocity-time curve.

Complete Step by step solution
We will find the work done in different portions of the graph.
Firstly, in portion OA:
$\Rightarrow$ ${v_O} = 0$ and ${v_A} = 10m{s^{ - 1}}$ (from graph)
We know, from work energy theorem
$W = {K_f} - {K_i}$
Woke done in moving from O to A,
$\Rightarrow$ ${W_{OA}} = {K_A} - {K_O} \\\ {W_{OA}} = \dfrac{1}{2}mv_A^2 - \dfrac{1}{2}mv_O^2 \\\$
Putting values, we get
$\Rightarrow$ ${W_{OA}} = \dfrac{1}{2} \times 1 \times {10^2} - 0 \\\ {W_{OA}} = 50J......(1) \\\$
Now work done in portion AB:
$\because {v_A} = {v_B} = 10m{s^{ - 1}}$ (from graph)
$\therefore {W_{AB}} = 0......(2)$
Now work done in portion BC:
$\Rightarrow$ ${v_B} = 10m{s^{ - 1}}$ and ${v_C} = 0$ (from graph)
Hence work done in moving from B to C is
$\Rightarrow$ ${W_{BC}} = {K_C} - {K_B}$
${W_{BC}} = \dfrac{1}{2}m{v_c}^2 - \dfrac{1}{2}mv_B^2$
Putting values, we get
$\Rightarrow$ ${W_{BC}} = 0 - \dfrac{1}{2} \times 1 \times {10^2} \\\ {W_{BC}} = - 50J......(3) \\\$
Hence total work under given graph is given by:
$W = {W_{OA}} + {W_{AB}} + {W_{BC}}$
Using equation (1), (2) and (3) we get
$\Rightarrow$ $W = 50 + 0 - 50 \\\ W = 0J \\\$
Hence, the required work done is $0J$.

Note the work energy theorem is valid for all types of forces. It is valid even if the forces are non-conservative in nature but principle of conservation of mechanical energy is not valid for non-conservative forces. It means that in order to change the kinetic energy of the system we have to apply force and it may be of any type.