Solveeit Logo
Login

Question

Question: A particle of mass \( 1kg \) & charge \( \dfrac{1}{3}\mu C \) is projected towards a non-conducting ...

A particle of mass 1kg1kg & charge 13μC\dfrac{1}{3}\mu C is projected towards a non-conducting fixed spherical shell having the same charge uniformly distributed on its surface. Find the minimum initial velocity of projection required if the particle just grazes the shell.

Explanation

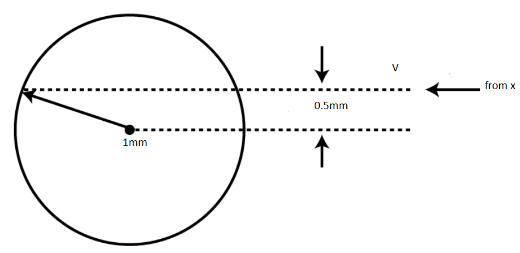
Solution

In order to solve this question, we are going to first apply the law of the conservation of momentum and find a relation for the final energy, then the law of conservation of energy is applied which on using the final velocity values thus found in the relation, which finally gives the minimum initial velocity.
According to the law of conservation of momentum,
mu=mvmu = mv
According to the law of conservation of energy:
Initial{\text{ }}kinetic{\text{ }}energy{\text{ }} = {\text{ }}work{\text{ }}done{\text{ }}in{\text{ }}bringing{\text{ }}the{\text{ }}particle{\text{ }}from{\text{ }}infinity{\text{ }} + {\text{ }}final{\text{ }}kinetic{\text{ }}energy \\\

Complete step by step answer:
Let us consider that the initial velocity is uu and the final velocity with which the shell is being grazed by the particle is vv . Now in the absence of the external torque, the conservation of the momentum is followed.
If the conservation of the momentum is applied across the shell, then the equation that follows is given as:
mu(0.5)=mv(1)mu\left( {0.5} \right) = mv\left( 1 \right)
Solving this, we get
v=u2v = \dfrac{u}{2}
Initial{\text{ }}kinetic{\text{ }}energy{\text{ }} = {\text{ }}work{\text{ }}done{\text{ }}in{\text{ }}bringing{\text{ }}the{\text{ }}particle{\text{ }}from{\text{ }}infinity{\text{ }} + {\text{ }}final{\text{ }}kinetic{\text{ }}energy \\\ \therefore \dfrac{1}{2}m{u^2} = \left( {\dfrac{{kq}}{R}} \right)q + \dfrac{1}{2}m{v^2} \\\
We can see that in this case, no energy is being lost, therefore, the conservation of energy can also be applied here:
Putting the values in this equation,
∴12(1)u2=(9×109×13×10−61×10−6)13×10−6+12(1)(u2)2\therefore \dfrac{1}{2}\left( 1 \right){u^2} = \left( {\dfrac{{9 \times {{10}^9} \times \dfrac{1}{3} \times {{10}^{ - 6}}}}{{1 \times {{10}^{ - 6}}}}} \right)\dfrac{1}{3} \times {10^{ - 6}} + \dfrac{1}{2}\left( 1 \right){\left( {\dfrac{u}{2}} \right)^2}
Now, if this equation is solved in the following way, we get
\dfrac{{{u^2}}}{2} = \left( {\dfrac{{3 \times {{10}^{ - 3}}}}{1}} \right)\dfrac{1}{3} \times {10^{ - 6}} + \dfrac{1}{2}\left( 1 \right)\dfrac{{{u^2}}}{4} \\\ \Rightarrow {u^2} = \dfrac{8}{3} \\\
Thus, the initial velocity comes out to be equal to:
u=223ms−1u = 2\sqrt {\dfrac{2}{3}} m{s^{ - 1}}
The minimum initial velocity of projection required if the particle just grazes the shell is 223ms−12\sqrt {\dfrac{2}{3}} m{s^{ - 1}}.

Note:
It is important to note that when the particle is projected towards a non-conducting fixed spherical shell having the same charge uniformly distributed on its surface, then the trajectory is such that it follows both the law of conservation of momentum as well as the law of conservation of energy.