Question

A particle of mass 100 g moves in xy plane such that its x-coordinate varies as x = 3sin2t and y coordinate varies as y = 3-3cos2t. (where t is time in sec and x and y in m). Find distance (in m) covered by particle in 2 seconds.

Answer 1

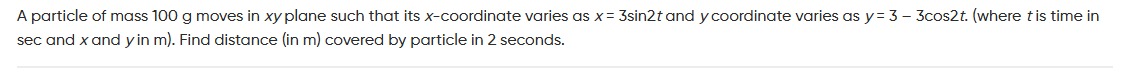
12 m

Answer 2

1. Calculate velocity components: Differentiate the given position coordinates with respect to time $t$. $x = 3\sin(2t) \implies v_x = \frac{dx}{dt} = \frac{d}{dt}(3\sin(2t)) = 3 \cdot \cos(2t) \cdot 2 = 6\cos(2t)$ m/s. $y = 3 - 3\cos(2t) \implies v_y = \frac{dy}{dt} = \frac{d}{dt}(3 - 3\cos(2t)) = 0 - 3 \cdot (-\sin(2t) \cdot 2) = 6\sin(2t)$ m/s.

2. Calculate speed: The speed $v$ of the particle is given by $v = \sqrt{v_x^2 + v_y^2}$. $v = \sqrt{(6\cos(2t))^2 + (6\sin(2t))^2} = \sqrt{36\cos^2(2t) + 36\sin^2(2t)}$ Using the trigonometric identity $\cos^2\theta + \sin^2\theta = 1$: $v = \sqrt{36(\cos^2(2t) + \sin^2(2t))} = \sqrt{36 \cdot 1} = 6$ m/s.

3. Calculate distance: The speed of the particle is constant ($6$ m/s). For constant speed, the distance covered is the product of speed and time. The time interval is given as $2$ seconds (from $t=0$ to $t=2$ s). Distance = Speed $\times$ Time Distance = $6 \text{ m/s} \times 2 \text{ s} = 12 \text{ m}$.

The mass of the particle (100 g) is not required for this kinematic calculation.