Question

A particle of mass $10{\text{ }}kg$ is suspended by two strings that make an angle of ${30^ \circ }$ and ${45^ \circ }$ respectively with the horizontal. Find tensions in the strings?

Answer 1

For finding tensions of the given strings we have to draw the free body diagram. Then with the help of horizontal components we will find the relation between both the tension in the strings. Then by substituting their value in the relation between the vertical components of the strings we will find the answer.

Complete step by step solution:
It is given in the question that a mass of $10{\text{ }}kg$ is suspended by two strings that make an angle of ${30^ \circ }$ and ${45^ \circ }$ respectively with the horizontal. So, we have to draw the free body diagram to solve this kind of problem.
The free body diagram of the given problem is-

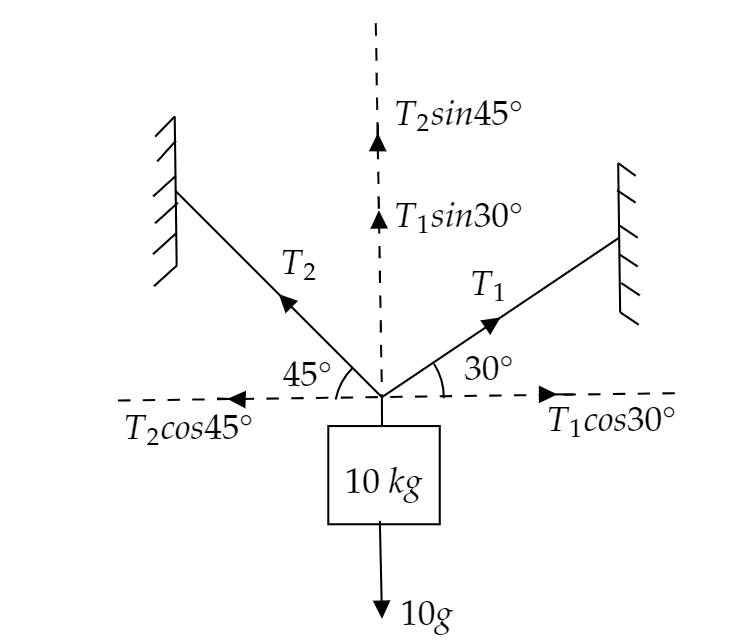
From the given diagram we have to formulate equations using vertical and horizontal components.
From the horizontal components we get,
${T_1}\cos {30^ \circ } = {T_2}\cos {45^ \circ }$
Substituting the values of the trigonometric identities we get,
${T_1}\dfrac{{\sqrt 3 }}{2} = {T_2}\dfrac{1}{{\sqrt 2 }}$
Arranging the equation we get,
${T_2} = \sqrt {\dfrac{3}{2}} {T_1} - - - - - \left( 1 \right)$
From the vertical components we get,
${T_1}\sin {30^ \circ } + {T_2}\sin {45^ \circ } = 10 \times g$
Let us consider acceleration due to gravity $g = 10{\text{ }}\dfrac{m}{{{s^2}}}$. So, we get,
$\dfrac{{{T_1}}}{2} + \dfrac{{{T_2}}}{{\sqrt 2 }} = 100$
Substituting the value of ${T_2}$ from equation $\left( 1 \right)$ we get,
$\dfrac{{{T_1}}}{2} + \dfrac{{\sqrt {\dfrac{3}{2}} {T_1}}}{{\sqrt 2 }} = 100$
Simplifying the equation we get,
$\left( {\sqrt 3 + 1} \right){T_1} = 200$
$\Rightarrow {T_1} = \dfrac{{200}}{{\sqrt 3 + 1}} = 73.20$
Substituting the value of ${T_1}$ in equation $\left( 1 \right)$ we get,
${T_2} = \sqrt {\dfrac{3}{2}} \times 73.20 = 89.66$
Hence, we find the tension in the strings are ${T_1} = 73.20{\text{ }}N$ and ${T_2} = 89.66{\text{ }}N$.

Note:
It must be noted that we have considered the value of acceleration due to gravity as $10{\text{ }}\dfrac{m}{{{s^2}}}$ for the ease of calculation. The original value of acceleration due to gravity is ${\text{9}}{\text{.8 }}\dfrac{m}{{{s^2}}}$. In case of horizontal components both are opposite and hence from the free body diagram they would balance each other. So, the horizontal components are considered to be equal.