Question

A particle of mass $1$ Kg carrying $0.01C$ charge is at rest on an inclined plane of angle ${30^ \circ }$ with the horizontal when an electric field of $\dfrac{{400}}{{\sqrt 3 }}{\text{N}}{{\text{C}}^{ - 1}}$ is applied parallel to the horizontal as shown. The coefficient of friction is:

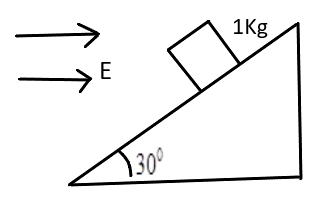
A) $0.5$
B) $\dfrac{1}{{\sqrt 3 }}$
C) $\dfrac{{\sqrt 3 }}{2}$
D) $\dfrac{{\sqrt 3 }}{7}$

Answer 1

Friction: It is defined as the opposing force acting on a body due to the presence of another body in contact when they are in motion.
Coefficient of friction: It is the relationship between two objects and the normal reaction between the objects that are in contact with each other.
First we will compare the forces on the inclined plane and later we will get the value of friction by substituting the values into the force along the vertical line formula.

Formula used:
Force due to electric field ${\text{ = qEcos}}\theta$
Here, q= charge of the electron, E=magnitude of electric field, θ= angle between the incline plane and horizontal plane
${\text{mg = f sin}}\theta {\text{ + Ncos}}\theta$, mg is the weight of the mass in downward direction
${\text{f = }}\mu {\text{N}}$, here, μ=coefficient of friction, N=normal force acting on the mass, f=frictional force

Complete step-by-step answer:
Given details, $E = \dfrac{{400}}{{\sqrt 3 }}{\text{N}}{{\text{C}}^{ - 1}}$, $\theta = {30^ \circ }$
Free body diagram of the mass resting on the inclined plane is shown in the figure,


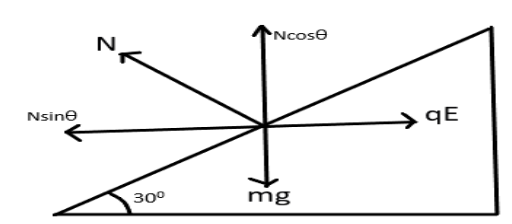
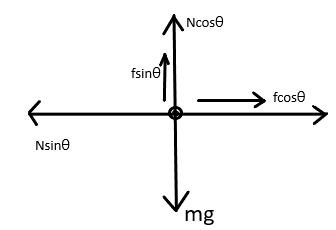
For the body to be at rest on the inclined plane, all the force acting on the body will be balanced with each other.
Comparing the forces on the inclined plane, we get,
${\text{qE cos}}\theta = \dfrac{400}{\sqrt 3} \times \dfrac{\sqrt 3}{2} \times 0.01$ = $2.45{\text{N}}$
${\text{mg sin}}\theta {{ = 1 \times 9}}{\text{.8}}\times \dfrac{1}{2}$ $= 4.9{\text{N}}$
We can say that, ${\text{qE sin}}\theta {\text{ < mg sin}}\theta$
From the above equation we can say that the motion is in the downward direction of the plane and f is up the inclined plane.
Force along the vertical direction gives, ${\text{mg = f sin}}\theta {\text{ + N cos}}\theta$
Substituting the above values in the equations, we get that, $1{\times {9}}{{.8 = f \times sin3}}{{\text{0}}^ \circ } + {\text{N cos3}}{{\text{0}}^ \circ }$
$\Rightarrow 9.8 = \dfrac{1}{2}{\text{f + }}\dfrac{{\sqrt 3 }}{2}{\text{N}}$
$\Rightarrow 19.6 = {\text{f + }}\sqrt 3 {\text{N}}$
The balancing force along the x-direction, ${\text{N sin}}\theta {\text{ = f cos}}\theta {\text{ + qE}}$
Substituting the above values in the equations, we get that, $\dfrac{1}{2}{\text{N = }}\dfrac{{\sqrt 3 }}{2}{\text{f + 245}}$
From the above two equations we get that, ${\text{f = }}\dfrac{{\sqrt 3 }}{7}{\text{N}}$

Hence the correct option is D.

Note: Free body diagram: It is the representation of the body on a plan that shows all the force acting on the body.
Electric field: It is defined as the region on which an electric charge has its effect.