Question

A particle of mass $1.6 \times {10^{ - 27}}\,{\text{kg}}$ and charge $1.60 \times {10^{ - 19}}\,{\text{coulomb}}$ enters in a uniform magnetic field of $1\,{\text{Tesla}}$ as shown in the fig. The speed of the particle is ${10^7}\,{\text{m/s}}$. The distance PQ will be:

A. $0.14\,{\text{m}}$
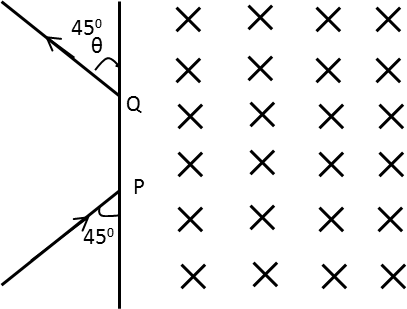
B. $0.28\,{\text{m}}$
C. $0.4\,{\text{m}}$
D. $0.5\,{\text{m}}$

Answer 1

Conclude the path of the particle in the magnetic field. Use the formula for the magnetic force and centripetal force to determine the radius of the circular path of the particle. Then determine the length of the distance PQ using the information of the angles given.

Formula used:
The magnetic force ${F_B}$ on the charge moving in the magnetic field is
${F_B} = qvB$ …… (1)
Here, $q$ is the charge, $v$ is the velocity of the charge and $B$ is the magnetic field.
The centripetal force ${F_C}$ on an object in circular motion is
${F_C} = \dfrac{{m{v^2}}}{R}$ …… (2)
Here, $m$ is the mass of the object, $v$ is the velocity of the object and $R$ is the radius of the circular path.

Complete step by step answer:
The mass of the particle is $1.6 \times {10^{ - 27}}\,{\text{kg}}$ and $1.60 \times {10^{ - 19}}\,{\text{coulomb}}$ is the charge on the particle.
$m = 1.6 \times {10^{ - 27}}\,{\text{kg}}$
$q = 1.60 \times {10^{ - 19}}\,{\text{coulomb}}$
The particle enters the magnetic field of $1\,{\text{Tesla}}$ with the speed ${10^7}\,{\text{m/s}}$.
$B = 1\,{\text{Tesla}}$
$v = {10^7}\,{\text{m/s}}$
The magnetic force acting on the particle gives the particle the necessary centripetal force and the particle starts moving in the circular path of radius $R$.
Determine the radius $R$ of the circular path of the particle.
Equate the magnetic force ${F_B}$ and the centripetal force ${F_C}$ on the particle is equal.
${F_B} = {F_C}$
Substitute $qvB$ for ${F_B}$ and $\dfrac{{m{v^2}}}{R}$ for ${F_C}$ in the above equation.
$qvB = \dfrac{{m{v^2}}}{R}$
$\Rightarrow qB = \dfrac{{mv}}{R}$
$\Rightarrow R = \dfrac{{mv}}{{qB}}$
Substitute $1.6 \times {10^{ - 27}}\,{\text{kg}}$ for $m$, ${10^7}\,{\text{m/s}}$ for $v$, $1.60 \times {10^{ - 19}}\,{\text{coulomb}}$ for $q$ and $1\,{\text{Tesla}}$ for $B$ in the above equation.
$R = \dfrac{{\left( {1.6 \times {{10}^{ - 27}}\,{\text{kg}}} \right)\left( {{{10}^7}\,{\text{m/s}}} \right)}}{{\left( {1.60 \times {{10}^{ - 19}}\,{\text{coulomb}}} \right)\left( {1\,{\text{Tesla}}} \right)}}$
$\Rightarrow R = 0.1\,{\text{m}}$
Hence, the radius of the circular path of the particle is $0.1\,{\text{m}}$.
Determine the distance PQ.
Draw the circular path of the particle.

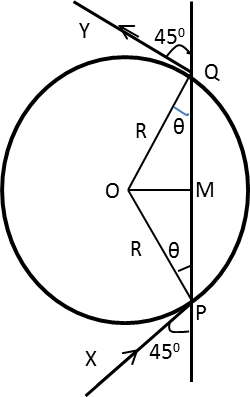
In the above figure, $45^\circ$ is the angle made by the particle with the horizontal line PQ.

Since the angle XPO and angle OQY are right angles, the angel $\theta$should be $45^\circ$.
Determine the value of PM in triangle OMP.
$\cos \theta = \dfrac{{{\text{PM}}}}{R}$
$\Rightarrow {\text{PM}} = R\cos \theta$
Determine the value of QM in triangle OMQ.
$\cos \theta = \dfrac{{{\text{QM}}}}{R}$
$\Rightarrow {\text{QM}} = R\cos \theta$
Determine the distance PQ.
The distance PQ is equal to the sum of the distance PM and MQ.
${\text{PQ}} = {\text{PM}} + {\text{MQ}}$
Substitute $R\cos \theta$ for ${\text{PM}}$ and $R\cos \theta$ for ${\text{MQ}}$ in the above equation.
${\text{PQ}} = \left( {R\cos \theta } \right) + \left( {R\cos \theta } \right)$
$\Rightarrow {\text{PQ}} = 2R\cos \theta$
Substitute $0.1\,{\text{m}}$ for $R$ and $45^\circ$ for $\theta$ in the above equation.
${\text{PQ}} = 2\left( {0.1\,{\text{m}}} \right)\cos 45^\circ$
$\therefore {\text{PQ}} = 0.142\,{\text{m}}$

Hence, the distance PQ is $0.142\,{\text{m}}$.

Note:
One cannot use the angle given with the velocity considering velocity components to determine the radius of the magnetic field as it is not the angle made by the direction of the particle with the magnetic field.