Question
Question: A particle of charge \(q\)and mass \(m\)is projected with a velocity \({{v}_{0}}\) towards a circul...
A particle of charge qand mass mis projected with a velocity v0 towards a circular region having a uniform magnetic field Bperpendicular and into the plane of paper from point P as shown in the figure. RIs the radius and O is the centre of that circular region. If the line OP makes an angle θ with the direction of v0 then the value of v0so that particle passes through O is
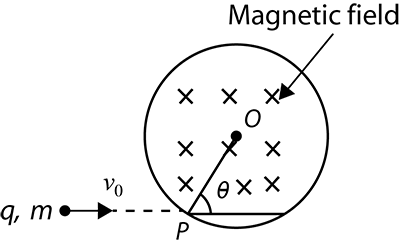
A.msinθqBRB.2msinθqBRC.msinθ2qBRD.2msinθ3qBR
Solution
Hint : trigonometry is used in order to solve this question. Basic trigonometry functions like sine, cosine are used up here. Radius of the circular path can be found by using sine function and rearranging it.
Complete step by step answer:
The sine function is a trigonometric function based on angle. This function of sine of an acute angle is explained on the basis of a right triangle. For a particular angle, it is the ratio of the length of the side that is opposite to that angle which may be altitude or base and to the length of the longest side of the triangle which is called a hypotenuse.
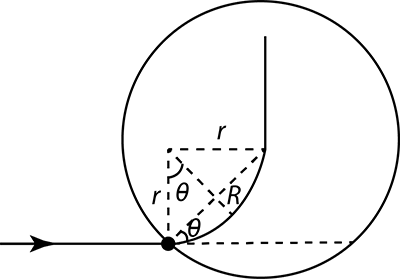
For this question, let rbe the radius of the circular path and v0=2msinθqBR
sinθ=r(2R)
Rearranging will give,
=2rR
As we all know the radius of curvature is given by
r=qBmv
Where mthe mass of the object is, vis the velocity, q is the charge and B is the magnetic field.
Substituting rwill give,
2sinθR=qBmv
Now rearranging the terms can make the equation,
v0=2msinθqBR
Therefore the correct answer is option B.
Note: one period of the sine wave is the length of one cycle of the wave. The period of the sine wave is 2π. Magnetic field is the region in space where we can experience magnetic properties. It will be probably around any charge or around any current carrying conductor.
