Question
Question: A particle of charge \( - q\) and mass \(m\)enters a uniform magnetic field \(\overrightarrow B \)(p...
A particle of charge −q and mass menters a uniform magnetic field B(perpendicular to the paper inwards) at P with a velocity vo at an angle α and leaves the field at Q with velocity v at an angle β as shown in the figure. Then
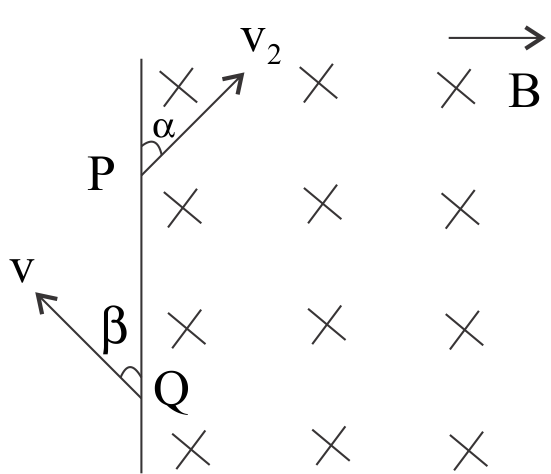
A. α=β
B. v=v0
C. PQ=Bq2mv0sinα
D. Particle remains in the field for time t=Bq2m(Π−α)
Solution
Hint When a uniform field is applied, the particle always describes a symmetric path. As the velocity of the particle is perpendicular to the magnetic field, it will describe a circular path. From this information we can calculate the radius of the circle and also the time taken to describe the circle.
Formula used
Fm=q(v×B) Where Fm is the magnetic force, acting on a particle of charge q moving with velocity v in a magnetic field B.
q(v0×B)=rmv02 where r is the radius of the circle described by the particle and m is the mass of the particle.
Complete step by step answer
Magnetic field can exert force on a moving charge or a current carrying conductor. This force can be given as,
Fm=q(v×B)
Where Fm is the force, acting on a particle of charge q moving with velocity v in a magnetic field B.
Along the magnetic force if there exists an electric field E, then the total electromagnetic force on the charge will be F=q[E+v×B]
This is called the Lorentz force.
The particle enters the magnetic field making an angle α
It’s given that the magnetic field is uniform in nature. So, the particle on entering the magnetic field assumes a circular path and exits the field making an angle β
As the magnetic field is uniform, so the angle of incidence and the angle of departure must be the same.
Therefore, α=β
Again, in a uniform magnetic field the velocity of the particle remains constant. Therefore, the velocity of the particle before entering and its velocity upon exiting the field must be the same.
Thus, we have v=v0
PQ is an arc of the circle describing the particle in the magnetic field.
For this circle, the centrifugal force must be equal to the magnetic force experienced by the particle
Which means,
q(v0×B)=rmv02 where r is the radius of the circle described by the particle.
⇒qv0B=rmv02 ⇒r=qBmv0 ( As the velocity of the particle is perpendicular to the direction of the magnetic field.)
So, the length of the arc PQ is given by 2rsinα=qB2mv0sinα
The time period to describe the complete circle is,
T=v02Πr ⇒T=qBv02Πmv0 ⇒T=qB2Πm
Where 2Πris the circumference of the circle.
Now, since the particle only describes the circle by an angle of 2α before the departs the field,
Time period of the particle inside the field is T×2Π(2Π−2α) =qB2Πm×2Π(2Π−2α)=qB(2Π−2α)m
Therefore, all the above options are correct.
Note: The particle describes a circular path in the given question as the velocity of the particle is perpendicular to the magnetic field. If it would have made an angle θ, then the particle would have described a helical path.
