Question
Question: A particle of charge +q and a mass m is moving under the influence of a uniform electric field E\[\w...
A particle of charge +q and a mass m is moving under the influence of a uniform electric field Ei and a uniform magnetic field Bk follows a trajectory from P to Q as shown below. The velocities at P and Q are Vi and −2j respectively. Which of the following statement(s) is/are correct?
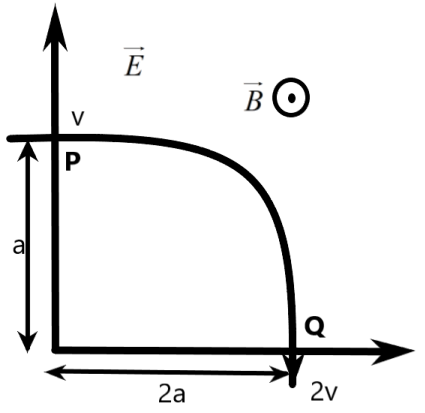
A) E=4qa3mv2
B) Rate of work done by electric fields at P is4a3mv2.
C) Rate of work done by the electric field at P is zero.
D) Rate of work done by both the fields at Q is zero.
Solution
We need to understand the dependence of the uniform magnetic field and the uniform electric field experience by a particle under motion on the trajectory of the particle to get the work done by the two fields that can solve this problem.
Complete Step-by-Step Solution:
We are given that a positively charged particle is moving with a speed along the horizontal direction and vertical direction in a uniform magnetic and electric field. We are asked to find the work done using the information on the trajectory and the velocity along the two directions.
We know that the energy possessed by the particle in motion is due to the kinetic energy provide by the electric field which can be found as the difference between the kinetic energies due to velocities perpendicular to each other as –
& KE=K{{E}_{y}}-K{{E}_{x}} \\\ & \Rightarrow KE=\dfrac{1}{2}m{{(-2v)}^{2}}-\dfrac{1}{2}m{{v}^{2}} \\\ & \therefore KE=\dfrac{3}{2}m{{v}^{2}} \\\ \end{aligned}$$  The work done by the electric field can be given as – $$\begin{aligned} & \text{From the electrostatic force,} \\\ & \text{Electrostatic energy = Electrostatic force }\times \text{ Distance } \\\ & \Rightarrow KE=F(2a) \\\ & \Rightarrow KE=qE2a \\\ & \Rightarrow E=\dfrac{KE}{2aq} \\\ & \therefore E=\dfrac{3m{{v}^{2}}}{4aq} \\\ \end{aligned}$$ This is the required solution for the work done by the electric field in total. At the points P and Q, the fields are perpendicular to the motion of the particle and therefore, there is no work by both the fields at those points. **The correct answers are options A, B and D.** **Note:** The work done by the fields are dependent on the displacement of the charge with the field. At point Q, the charge does not have a displacement along the parallel direction of the electric field and therefore, it becomes zero and at P there is no displacement.