Question

A particle of charge $- 16 \times {10^{ - 18}}\,C$ moving with velocity 10 m/s along the X-axis enters region where a magnetic field of induction B is along Y-axis and field of magnitude ${10^4}\,V/m$ is along negative Z-axis. If the charged particle continuous moving along the X-axis, the magnitude of B is:

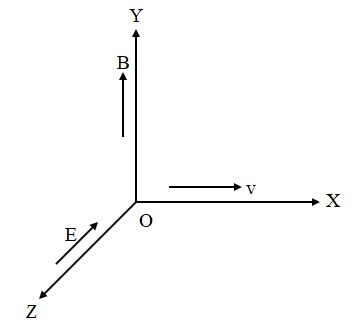
A. ${10^6}\,Wb/{m^2}$
B. ${10^5}\,Wb/{m^2}$
C. ${10^3}\,Wb/{m^2}$
D. ${10^7}\,Wb/{m^2}$

Answer 1

The particle continues to move along the X-axis implies that there is no net force along Z-axis and Y-axis. In that case, the electric force equals the magnetic force on the particle.
Formula used:
${F_e} = qE$
Here, q is the charge of the particle.
${F_B} = qvB$
Here, v is the velocity of the particle.

Complete step by step answer:
We know that the electric force acting on the charged particle placed in the uniform electric field $E$ is,
${F_e} = qE$
Here, q is the charge of the particle.
Also, the magnetic force on the particle placed in the magnetic field $B$ is,
${F_B} = qvB$
Here, v is the velocity of the particle.
Since the particle continues to move along the X-axis, the electric force along the negative Z-axis is equal to the magnetic force on the particle along the Y-axis. The net force on the particle is zero except along the X-axis.
Therefore, we can write,
$qE = qvB$
$\Rightarrow B = \dfrac{E}{v}$
Substitute ${10^4}\,V/m$ for E and 10 m/s for v in the above equation.
$B = \dfrac{{{{10}^4}}}{{10}}$
$\Rightarrow B = {10^3}\,Wb/{m^2}$

So, the correct answer is “Option C”.

Note:
If the electric force along the negative Z-axis does not equal the magnetic force along the Y-axis, the particle could have moved along the direction whichever the force has maximum value. The unit of magnetic field is Tesla or $Wb/{m^2}$, therefore, if the magnetic field is given in Tesla, we don’t need to convert it into S.I. unit.