Question

A particle moving with uniform acceleration has average velocities $v_{1},v_{2}andv_{3}$ over the successive intervals of time $t_{1},t_{2}andt_{3}$ respectively. The value of $\frac{(v_{1} - v_{2})}{(v_{2} - v_{3})}$will be

• A. $\frac{t_{1} - t_{2}}{t_{2} - t_{3}}$
• B. $\frac{t_{1} - t_{2}}{t_{2} + t_{3}}$
• C. $\frac{t_{1} + t_{2}}{t_{2} - t_{3}}$
• D. $\frac{t_{1} + t_{2}}{t_{2} + t_{3}}$

Answer 1

Answer: (D)

$\frac{t_{1} + t_{2}}{t_{2} + t_{3}}$

Answer 2

Let u be initial velocity and a be uniform accelerations.

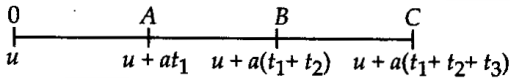
Average velocities in the intervals from 0 to $t_{1},t_{1}$to $t_{2}$and $t_{2}$to $t_{3}$are

$v_{1} = \frac{u + u + at_{1}}{2} = u + \frac{a}{2}t_{1}$ …….. (i)

$v_{2} = \frac{u + at_{1} + u + a(t_{1} + t_{2})}{2} = u + at_{1} + \frac{a}{2}t_{2}$ ….. (ii)$v_{3} = \frac{u + a(t_{1} + t_{2}) + u + a(t_{1} + t_{2} + t_{3})}{2}$

$= u + at_{1} + at_{2} + \frac{a}{2}t_{3}$ ……….(iii)

Subtract (i) Form (ii), we get

$v_{2} - v_{1} = \frac{a}{2}\left( t_{1} + t_{2} \right)$ …….. (iv)

Subtract (ii) from (iii), we get

$v_{3} - v_{2} = \frac{a}{2}\left( t_{2} + t_{3} \right)$ ……… (v)

Divide (iv) by (v) , we get

$\frac{v_{2} - v_{1}}{v_{3} - v_{2}} = \frac{(t_{1} + t_{2})}{(t_{2} + t_{3})}or\frac{v_{1} - v_{2}}{v_{2} - v_{3}} = \frac{(t_{1} + t_{2})}{(t_{2} + t_{3})}$