Question

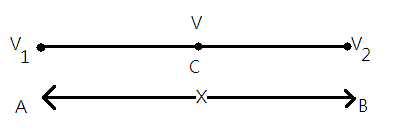
A particle moving with uniform acceleration from A to B along a straight line has velocities ${v_1}$ and ${v_2}$ at A and B, respectively. If C is the mid-point between A and B, then determine the velocity of the particle at C.

A) $v = \sqrt {\dfrac{{{v_1}^2 + {v_2}^2}}{3}}$
B) $v = \sqrt {\dfrac{{{v_1}^2 + {v_2}^2}}{2}}$
C) $v = \sqrt {\dfrac{{{v_1}^2 + {v_2}^2}}{4}}$
D) $v = \sqrt {\dfrac{{{v_1}^2 + {v_2}^2}}{{8}}}$

Answer 1

In this problem, it is given that a particle travels from a point A to point B with uniform acceleration. We are required to find the velocity of the particle at mid-point of the journey. Apply the kinematical equation from point A to C and then from point C to B. The distance travelled is the same in both cases. Equating both the equations, we can find the velocity at the midpoint.

Complete step by step solution:
Let us consider the total distance between A and B is $x$ units. As, C is the midpoint of AB thus, the distance $AC = CB = \dfrac{x}{2}$. We are given with the initial velocity at A to be ${v_1}$ and let the acceleration of the particle be $'a'\,m{s^{ - 2}}$.
Let the velocity at point C will be $v$ , from kinematical equation we have:
${v^2} - {v_1}^2 = 2a\dfrac{x}{2}$
$\Rightarrow {v^2} - {v_1}^2 = ax$--equation $1$
Also, we are given with the final velocity at B to be ${v_2}$ and the acceleration of the particle remains constant, $'a'\,m{s^{ - 2}}$
The displacement is $\dfrac{x}{2}$
For motion between point C and D, the initial velocity of the particle is the velocity at point C, $v$ :
Applying kinematical equation between point C, we have
${v_2}^2 - {v^2} = 2a\dfrac{x}{2}$
$\Rightarrow {v_2}^2 - {v^2} = ax$--equation $2$
From equation $1$ and equation $2$ , we have
${v^2} - {v_1}^2 = {v_2}^2 - {v^2}$
$\Rightarrow {v^2} + {v^2} = {v_2}^2 + {v_1}^2$
$\Rightarrow 2{v^2} = {v_2}^2 + {v_1}^2$
$\Rightarrow {v^2} = \dfrac{{{v_2}^2 + {v_1}^2}}{2}$
$\Rightarrow v = \sqrt {\dfrac{{{v_2}^2 + {v_1}^2}}{2}}$
This is the velocity of the particle at point C.

Thus, option B is the correct option.

Note: The velocity at C is not the average of the initial and final velocity as the particle is having a constant acceleration thus, its velocity is constantly changing. While applying the kinematical equation between C and B, the initial velocity is the velocity at point C and the final velocity is the velocity at point B.