Question

A particle moving on a straight line ultimately comes to rest. What is the angle between its
initial velocity and acceleration?​
A) Zero
B) 45°
C) 90°
D) 180°

Answer 1

We can assume a moving body and then observe the variations of velocities according to the question graphically so as to calculate the required angle.
Relationship between acceleration and velocity is given as:
$a = \dfrac{{du}}{{dt}}$
Rate of change of velocity is defined as acceleration and its units are $m/{s^2}$

Complete step by step answer: Let a particle move with an initial velocity u and acceleration a.
The object finally comes to rest, this means its final velocity (v) will be zero
$\Rightarrow$ v = 0
If we plot a velocity – time graph it will be:

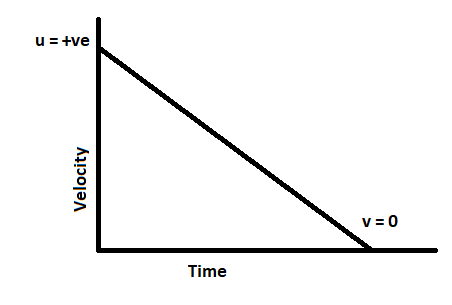
Here,
u has any positive value which finally decreases and becomes zero with respect to time.
Now, the slope (S) of any graph is the change in quantity on y – axis with respect to the x-axis:
$S = \dfrac{{dy}}{{dx}}$
In this case the slope will be $\dfrac{{du}}{{dt}}$; rate of change of velocity
And,
Acceleration is defined as the rate of change of velocity:
$a = \dfrac{{du}}{{dt}}$
Thus, the slope of this graph represents acceleration.
We can see that the slope is degrading and hence have a negative value
$\Rightarrow$ a = -ve
For positive initial velocity, the acceleration of a body is negative:

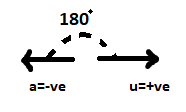
As both are in opposite directions, the angle formed between them is 180°
Therefore, the angle between the initial velocity and acceleration of the given particle is 180° and the correct option is D)

Note: ‘Rate’ is always measured with respect to the time.
The derivatives show the change in respective quantities. E.g.
If x = ${x_1} - {x_2}$; then this will also be equal to dx.
The graph basically shows variation of one quantity with respect to the other