Question

A particle moving along a straight line covers half of the distance with a speed of $3m{{s}^{-1}}$. The other half of the distance is covered in two equal time intervals with speed of $4.5m{{s}^{-1}}$and $7.5m{{s}^{-1}}$. The average speed of the particle (in $m{{s}^{-1}}$) is
$\begin{aligned} & A.5.0 \\\ & B.5.5 \\\ & C.5.8 \\\ & D.4.0 \\\ & E.4.8 \\\ \end{aligned}$

Answer 1

Hint: We can work on the above question by dividing the question in two parts. Because the particle is travelling half the distance with some speed and the other half with other speed in equal time intervals. In the first part we will calculate the average speed that particle travelling in two equal time intervals and in the second part we will calculate the average speed of the entire journey.

Complete step by step answer:
To proceed further let us know some definitions related to our question.
Speed: The distance travelled by particle in unit time is known as speed.
Speed is a scalar quantity i.e. it has only magnitude but no direction and speed is always positive for a moving particle.
Distance: The length of the path travelled by a particle is known as distance.
Distance is a scalar quantity and is always positive for a moving particle.
Average speed: It is the ratio of total distance travelled by the particle to the total time taken to cover that distance.
Now, let us move to our question.
We know that average speed is given by:
$\begin{aligned} & {{v}_{AD}}=\dfrac{s}{\left( \dfrac{s}{2{{v}_{AB}}} \right)+\left( \dfrac{s}{2{{v}_{BD}}} \right)} \\\ & {{v}_{AD}}=\dfrac{2{{v}_{AB}}{{v}_{BD}}}{{{v}_{AB}}+{{v}_{BD}}} \\\ & {{v}_{AD}}=\dfrac{2\times 3\times 6}{3+6} \\\ & {{v}_{AD}}=4m{{s}^{-1}} \\\ \end{aligned}$ ${{v}_{average}}=\dfrac{s}{t}$
Where:
${{v}_{average}}=$average speed
$s=$total distance
$t=$ total time
We are dividing the above problem in two parts, first we calculate the average speed when the particle is moving with different velocity in equal interval of time.
Total Distance is divided in two equal parts. Let the total distance be $s$

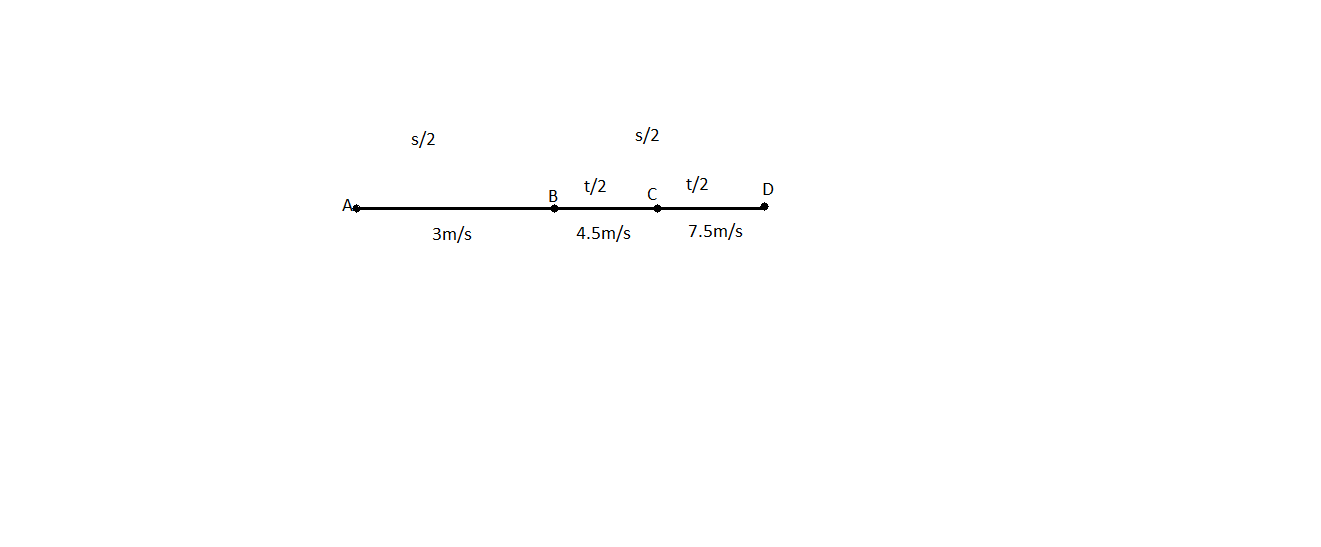
Average speed from B to D, that is particle travelling in equal time interval is given by:
$\begin{aligned} & {{v}_{BD}}=\dfrac{{{v}_{1}}\dfrac{t}{2}+{{v}_{2}}\dfrac{t}{2}}{t} \\\ & {{v}_{BD}}=\dfrac{{{v}_{1}}+{{v}_{2}}}{2} \\\ & {{v}_{BD}}=\dfrac{4.5+7.5}{2} \\\ & {{v}_{BD}}=\dfrac{12}{2} \\\ & {{v}_{BD}}=6m{{s}^{-1}} \\\ \end{aligned}$
Now calculating average speed of the whole journey:
$\begin{aligned} & {{v}_{AD}}=\dfrac{s}{\left( \dfrac{s}{2{{v}_{AB}}} \right)+\left( \dfrac{s}{2{{v}_{BD}}} \right)} \\\ & {{v}_{AD}}=\dfrac{2{{v}_{AB}}{{v}_{BD}}}{{{v}_{AB}}+{{v}_{BD}}} \\\ & {{v}_{AD}}=\dfrac{2\times 3\times 6}{3+6} \\\ & {{v}_{AD}}=4m{{s}^{-1}} \\\ \end{aligned}$
Hence, the average velocity through the entire journey is $4m{{s}^{-1}}$.
Hence, the correct answer is option D.

Note: Students can deal with this type of problem by dividing them into smaller parts. So that it becomes easy to calculate the average speed.
If the particle travels the distance in equal time intervals then the average speed of the particle is simply the average of individual speed.