Question

A particle moves through angular displacement $\theta$ on a circular path of radius r. The linear displacement will be:
A) $2r\sin \left( {\dfrac{\theta }{2}} \right)$.
B) $2r\cos \left( {\dfrac{\theta }{2}} \right)$.
C) $2r\tan \left( {\dfrac{\theta }{2}} \right)$.
D) $2r\cot \left( {\dfrac{\theta }{2}} \right)$.

Answer 1

A displacement is defined as the shortest distance between the intimal and final position. The angular displacement is the displacement on the circular track which is represented by angle which is$\theta$ whereas linear displacement will be the shortest distance between the initial and the final point on the circular point.

Formula Used: The formula for the linear displacement is given by,
$\Rightarrow \Delta \vec r = \sqrt {{r_2}^2 + {r_1}^2 - 2{r_1}{r_2}\cos \theta }$

Complete step by step answer:
It is given in the problem that a particle moves through angular displacement $\theta$ on a circular path of radius r and we need to find the linear displacement between the initial and the final position of the body.
As it is given that the angle between the initial and final position or the angular displacement is given to be$\theta$. Let the initial position vector be ${\vec r_1}$ and the final position vector is ${\vec r_2}$ and the points on the circle be A and B respectively.

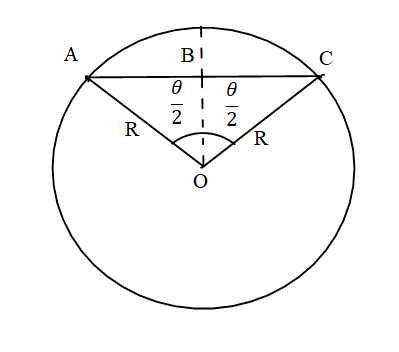
Here the linear displacement is equal to AC. Let us calculate the value of AC from both of the triangle ABO and triangle BCO.
In triangle ABO,
$\Rightarrow \sin \left( {\dfrac{\theta }{2}} \right) = \dfrac{{AB}}{R}$
$\Rightarrow AB = R\sin \left( {\dfrac{\theta }{2}} \right)$………eq. (1)
In triangle BCO,
$\Rightarrow \sin \left( {\dfrac{\theta }{2}} \right) = \dfrac{{BC}}{R}$
$\Rightarrow BC = R\sin \left( {\dfrac{\theta }{2}} \right)$………eq. (2)
Since, $AC = AB + BC$.
Replacing the values of AB and BC from the equation (1) and equation (2) in the above equation.
$\Rightarrow AC = AB + BC$
$\Rightarrow AC = \left[ {R\sin \left( {\dfrac{\theta }{2}} \right)} \right] + \left[ {R\sin \left( {\dfrac{\theta }{2}} \right)} \right]$
$\Rightarrow AC = 2 \cdot R\sin \left( {\dfrac{\theta }{2}} \right)$.
The linear displacement will be equal to$AC = 2 \cdot R\sin \left( {\dfrac{\theta }{2}} \right)$. The correct answer is option A.

Note: It is advisable to the students to understand and remember the formula of the vector addition or subtraction as it can help in solving these kinds of problems. The angle $\theta$ is between the line joining the initial and the final position with the center of the circle.