Question

A particle moves on a circular path of radius, R. Find magnitude of its displacement during an interval in which it covers an angle$\theta$
(A) $R\theta$
(B) $R\sin \theta$
(C) $2R\cos \left( {\dfrac{\theta }{2}} \right)$
(D) $2R\sin \left( {\dfrac{\theta }{2}} \right)$

Answer 1

Hint : Displacement is the length of shortest route between the initial position and final position. The shortest route can be found out by drawing a straight line from initial position to final position. In addition to this we use trigonometric ratios to find out the length of the straight line drawn from initial to final position.

Complete step by step solution:
In the following diagram, we can see the path followed and the shortest route.

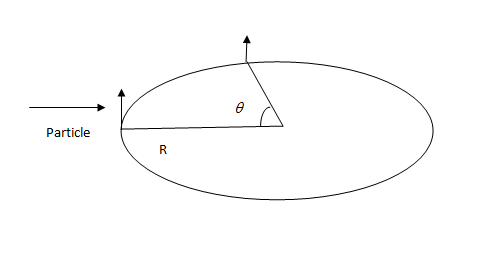
Here, arch from A to B is the distance and the straight-line joining A and B is the displacement.
Geometrically, a perpendicular dropped on a chord like AB, bisects the chord i.e., divides it into two equal parts.
AC=BC
AB=2AC=2BC
OB=R (radius)
In triangle OBC, using trigonometric ratio for the right angled triangle formed by bisecting the chord by a line passing through the center.
$\sin (\dfrac{\theta }{2}) = \dfrac{{BC}}{{OB}}$
$\Rightarrow BC = OB\sin (\dfrac{\theta }{2}) \\\ \Rightarrow BC = R\sin (\dfrac{\theta }{2}) \\\ \\\$
Now,
AB=2BC
$AB = 2R\sin (\dfrac{\theta }{2})$
Since, we have found the length of straight line joining initial and final position, it gives the displacement of the body moving along the arch of the circle.
Hence, the displacement is $2R\sin (\dfrac{\theta }{2})$.
Therefore, the answer is (D).

Note: As the particle moves along the circle along the arch joining A and B, distance is the length of arch. As distance is the length of the path travelled by the body. We take distance d = R (. Therefore, you must not confuse this question between distance and displacement. A good knowledge of trigonometric ratios for right angled triangles is also important for this question.