Question

A particle moves on a circle of radius $r$ with centripetal acceleration as function of time as ${a_c} = {k^2}r{t^2}$ where $k$ is a positive constant .Find the following quantities as a function of time at an instant.
(A) The speed of the particle.
(B) The tangential acceleration of the particle
(C) the resultant acceleration and
(D) Angle made by the resultant with tangential direction

Answer 1

Hint : Use the formula for centripetal acceleration as well as tangential acceleration. The magnitude of centripetal acceleration is given by, ${a_c} = \dfrac{{{v^2}}}{r}$ where, $v$ is the linear velocity of the particle and $r$ is the radius of the path or circle. The tangential acceleration is given by, ${a_t} = \dfrac{{dv}}{{dt}}$ .

Complete Step By Step Answer:
We know that if a particle moves in a circle with velocity it will have an acceleration due to the change of its direction. The centripetal acceleration is the acceleration that acts towards the centre whereas the tangential acceleration acts along the tangent of the path hence the name.

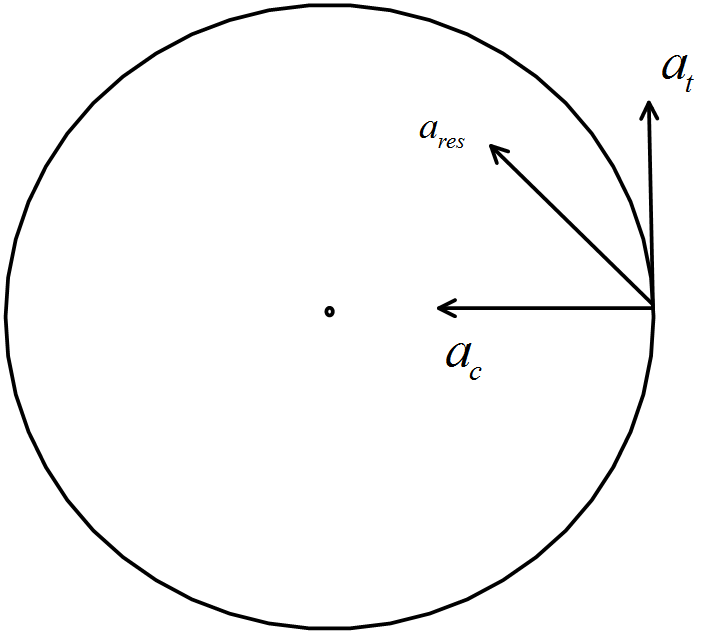
(a)Now we know that the magnitude of centripetal acceleration is given by, ${a_c} = \dfrac{{{v^2}}}{r}$ where, $v$ is the linear velocity of the particle and $r$ is the radius of the path or circle.
Here, we have the centripetal acceleration as, ${a_c} = {k^2}r{t^2}$ .
So, equating this with the equation of centripetal acceleration we get,
$\dfrac{{{v^2}}}{r} = {k^2}r{t^2}$
Or, ${v^2} = {k^2}{r^2}{t^2}$
Taking square root on both sides we get,
$v = krt$ .
So, velocity of the particle is $krt$
(b) We know that the tangential acceleration is given by, ${a_t} = \dfrac{{dv}}{{dt}}$
Hence, differentiating $v$ with respect to time we get,
${a_t} = \dfrac{{dv}}{{dt}} = \dfrac{d}{{dt}}\left( {krt} \right) = kr$
Hence, the tangential acceleration of the particle is $kr$
(c) the resultant acceleration of the particle is the magnitude of the net acceleration, ${a_{res}} = \sqrt {a_c^2 + a_t^2}$
hence, putting the values we get, ${a_{res}} = \sqrt {{{\left( {{k^2}r{t^2}} \right)}^2} + {{\left( {kr} \right)}^2}}$
Or, ${a_{res}} = kr\sqrt {{k^2}{t^4} + 1}$
Hence the resultant acceleration of the particle is , $kr\sqrt {{k^2}{t^4} + 1}$
(d) We know the tangent of the angle between the angle made by resultant acceleration with tangential acceleration is given by, $\tan \theta = \dfrac{{{a_c}}}{{{a_t}}}$
Hence, putting the values we get, $\tan \theta = \dfrac{{{k^2}r{t^2}}}{{kr}} = k{t^2}$ .
Therefore, the angle made by the resultant acceleration is $\theta = {\tan ^{ - 1}}\left( {k{t^2}} \right)$ .

Note :
The centripetal acceleration here is only a function of time and tangential acceleration is a constant or since the radius of the circle is a constant. So, the particle actually speeds up with time hence it also has a linear acceleration.