Question
Question: A particle moves in the x-y plane with the velocity \(\vec{v}=\hat{a}i+b\hat{x}j\) where a and b are...
A particle moves in the x-y plane with the velocity v=a^i+bx^j where a and b are constants. Initially, the particle was at the origin. The trajectory of the particle is.
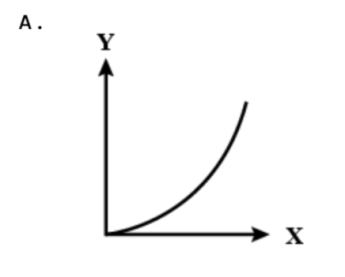
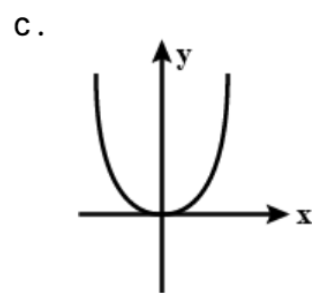
Solution
First take out all the possible things that are given in the question, like the particles are in origin that is x=0, y=0, Then we have to find the equation of the trajectory which will reveal the type of graph then we need the radius of curvature to finalize the graph.
Complete step-by-step answer:
We can write a vector v in the form of,
v=dtdxi^+dtdyj^
We know that the velocity of the particle is,
v=a^i+bx^j,
So on comparing the equations on the upper hand we can say that,
dtdx=a, and dtdy=bx
We know, dtdx=a
dx=adt
⇒∫dx=∫adt (integrating on both sides)
⇒x=at ……… Eq.1
We also know that, dtdy=bx
dtdy=bat ………(from Eq.1)
⇒dy=batdt
⇒∫dy=∫batdt (integrating on both sides)
Now,
y=21abt2 ………Eq.2
On comparing Eq.1 and Eq.2, we get,
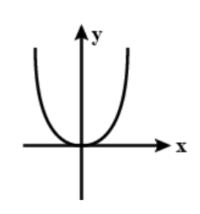
y=2abx2 , This is the trajectory of the particle.
Answer is option (c)
Additional Information:
A curve is a line smooth in nature that does not take sharp turns to deviate; it deviates gradually resulting in an upward or downward curve.
A trajectory is the path that an object with mass in motion follows through space as a function of time. In classical mechanics, the mass might be a projectile or a satellite.
Origin is the starting point from which a body starts to move. It is generally taken as (0,0).
A graph usually depicts a body’s certain known values at a fixed time, using a graph we can derive the velocity, mass, acceleration, etc at point time. A curve is generally made to predict the pathway of a particle, not generally a particle but rockets, spaceships, planets and many other things also.
Note: Which equation results in what curve is a must know, students often make calculation mistakes, definition of origin. Y is taken as a function of x to get the equation of the curve. Compare the values with vector values properly, only then we can get the answer(dx/dt=a).
