Question

A particle moves in a circle of radius $R$ with a constant speed $v$. Then, find the magnitude of average acceleration during a time interval $\dfrac{{\pi R}}{{2v}}$.

Answer 1

Use the formula for average acceleration of a particle in terms of average velocity and time. Then using the formula for the time period of the particle, determine the total path travelled by the particle in the given time interval. Draw the path of the particle on the circle and determine the average velocity of the particle. Then using the formula, determine the average acceleration of the particle.

Formula used:
The average acceleration ${a_{avg}}$ of an object is given by
${a_{avg}} = \dfrac{{{v_{avg}}}}{t}$ …… (1)
Here, ${v_{avg}}$ is the average velocity of the object and $t$ is the time.

Complete step by step answer:
We have given that the radius of the circle in which the particle moves with constant speed $v$ is $R$.We have asked to calculate the average acceleration of the particle in the interval $\dfrac{{\pi R}}{{2v}}$.
$t = \dfrac{{\pi R}}{{2v}}$
Let us first determine the path of the circumference travelled by the particle.The time $T$ required for the particle to complete one circle is given by
$T = \dfrac{{2\pi R}}{v}$
So the path on the circle travelled by the particle is
$s = \dfrac{t}{T}$
$\Rightarrow s = \dfrac{{\dfrac{{\pi R}}{{2v}}}}{{\dfrac{{2\pi R}}{v}}}$
$\Rightarrow s = \dfrac{1}{4}$
Hence, the particle has travelled one fourth of the total circle.

Let us draw the diagram of the circle with the velocities of the particle.

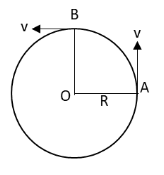
From the above equation, the particle travels from point A to B.

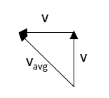
Thus, the average velocity is given by
${v_{avg}} = \sqrt {{{\left( v \right)}^2} + {{\left( { - v} \right)}^2}}$
$\Rightarrow {v_{avg}} = \sqrt 2 v$
Hence, the average velocity of the particle is $\sqrt 2 v$.
Let us now calculate the average acceleration of the particle.Substitute $\sqrt 2 v$ for ${v_{avg}}$ and $\dfrac{{\pi R}}{{2v}}$ for $t$ in equation (1).
${a_{avg}} = \dfrac{{\sqrt 2 v}}{{\dfrac{{\pi R}}{{2v}}}}$
$\therefore {a_{avg}} = \dfrac{{2\sqrt 2 {v^2}}}{{\pi R}}$

Hence, the average velocity of the particle is $\dfrac{{2\sqrt 2 {v^2}}}{{\pi R}}$.

Note: One can also solve the same question by another method. One can determine the average force acting on the particle by using the formula in terms of change in momentum and time. Then one can use the formula for the average force in terms of the mass and average acceleration of the particle. From which one can determine the average acceleration of the particle.